题目内容
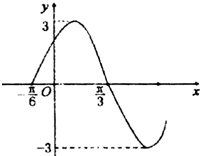
如图所示是y=Asin(ωx+φ)的图象(其中A>0,ω>0,|φ|≤
)一部分,则其解析表达式为( )
| π |
| 2 |

A、y=3cos(2x+
| ||
B、y=3cos(2x-
| ||
C、y=3sin(2x+
| ||
D、y=3sin(2x-
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:函数的性质及应用
分析:由图象可知,函数的最大值为3,所以A=3;由两个零点可知函数的半个周期为
-(-
)=
,可得周期为π,由周期公式可得ω,将(-
,0)代入解析式,可求φ.
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
解答:
解:由图象可知函数的最大值为3,
所以A=3,
可知半个周期为
-(-
)=
,
所以周期为π,
所以
=π,∴ω=2,
将(-
,0)代入解析式可知φ=
,
所以解析式为y=3sin(2x+
);
故选C.
所以A=3,
可知半个周期为
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
所以周期为π,
所以
| 2π |
| ω |
将(-
| π |
| 6 |
| π |
| 3 |
所以解析式为y=3sin(2x+
| π |
| 3 |
故选C.
点评:本题考查了由三角函数图象求解析式的问题;此类题目,一般是由图象的最高点和最低点的纵坐标差值求最值,求A,由周期求ω,最后代人特殊值求φ,还要注意各参数的取值范围.

练习册系列答案
相关题目
若角β的终边经过点P(1,-2),则sinβ的值是( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
关于方程|log2x|=lg(x+1)的两个根x1,x2(x1<x2)以下说法正确的是( )
| A、x1+x2>2 |
| B、x1x2>2 |
| C、0<x1x2<1 |
| D、1<x1+x2<2 |
函数f(x)=x2-3x+2在区间(1,2)内的函数值为( )
| A、大于等于0 | B、等于0 |
| C、大于0 | D、小于0 |
某设备的使用年限x与所支出的总费用y(万元)统计数据如下表
据上表可得回归方程
=
x+
中的
=0.7,据此预测设备使用年限为6年时总费用为( )
| 使用年限x | 1 | 2 | 3 | 4 |
| 总费用y | 1.5 | 2 | 3 | 3.5 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| A、4.95万元 |
| B、5.2万元 |
| C、4.35万元 |
| D、4.9万元 |
已知正项等比数列{an}的前n项和为Sn,bn=
,且{bn}的前n项和为Tn,若对一切正整数n都有Sn>Tn,则数列{an}的公比q的取值范围是( )
| a3n |
| a2n+1 |
| A、0<q<1 | ||
| B、q>1 | ||
C、q>
| ||
D、1<q<
|