题目内容
13.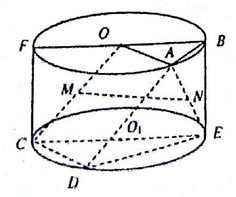 如图,矩形FCEB是圆柱OO1的轴截面,且FC=1,FB=2,点A、D分别在上下底面圆周上,且在面FCEB的同侧,△OAB是等边三角形,∠ECD=60°,M、N分别是OC、AE的中点.
如图,矩形FCEB是圆柱OO1的轴截面,且FC=1,FB=2,点A、D分别在上下底面圆周上,且在面FCEB的同侧,△OAB是等边三角形,∠ECD=60°,M、N分别是OC、AE的中点.(1)求证:MN∥面CDE;
(2)求二面角C-AD-E的余弦值.
分析 (1)由∠ECD=∠BOA=60°,得OA∥CD,且OA=CD,从而四边形CDAO是平行四边形,取AD中点G,连结MG、NG,推导出平面MGN∥面CDE,由此能证明MN∥面CDE.
(2)以C为原点,在平面CDE是过C作CE的垂线为x轴,CE为y轴,CF为z轴,建立空间直角坐标系,利用向量法能求出二面角C-AD-E的余弦值.
解答 证明:(1)如图,由∠ECD=∠BOA=60°,得OA∥CD,且OA=CD,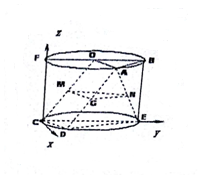
∴四边形CDAO是平行四边形,
取AD中点G,连结MG、NG,则MG∥CD,NG∥DE,MG∩NG=G,
∴平面MGN∥面CDE,
∵MN?面MNG,∴MN∥面CDE.
解:(2)以C为原点,在平面CDE是过C作CE的垂线为x轴,CE为y轴,CF为z轴,建立空间直角坐标系,
∵FC=1,FB=2,∴C(0,0,0),D($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),
A($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$,1),E(0,2,0),
$\overrightarrow{CD}$=($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),$\overrightarrow{DA}$=(0,1,1),$\overrightarrow{DE}$=(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$,0),
设平面CAD的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CD}=\frac{\sqrt{3}}{2}x+\frac{1}{2}y=0}\\{\overrightarrow{n}•\overrightarrow{DA}=y+z=0}\end{array}\right.$,取x=$\sqrt{3}$,得$\overrightarrow{n}$=($\sqrt{3},-3,3$),
同理,得到平面ADE的法向量为$\overrightarrow{m}$=($\sqrt{3},1,-1$),
设二面角C-AD-E的平面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{3}{\sqrt{21}•\sqrt{5}}=\frac{\sqrt{105}}{35}$,
∴二面角C-AD-E的余弦值为$\frac{\sqrt{105}}{35}$.
点评 本题考查线面平行的证明,考查二面角的余弦值的求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,是中档题.

| A. | ±4 | B. | -4 | C. | 4 | D. | 5 |
| A. | -$\frac{3\sqrt{7}}{7}$ | B. | $\frac{3\sqrt{7}}{7}$ | C. | $\frac{\sqrt{7}}{3}$ | D. | -$\frac{\sqrt{7}}{3}$ |
 已知全集U=R,集合A={x|x2-2x≤0},B={y|y=sinx,x∈R},则图中阴影部分表示的集合为( )
已知全集U=R,集合A={x|x2-2x≤0},B={y|y=sinx,x∈R},则图中阴影部分表示的集合为( )| A. | [-1,2] | B. | [-1,0)∪(1,2] | C. | [0,1] | D. | (-∞,-1)∪(2,+∞) |
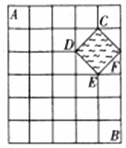 如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.
如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.