题目内容
18.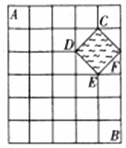 如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.
如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.
分析 本题可以结合图形,分类来解题,因为在湖边有两个菱形的边走时是最短距离,即走A→CF→B,A→DE→B,根据分类加法原理得到结果.
解答 解:由题意知本题有两种途径是最短的路程,
①A→CF→B其中A→C有5法.F→B有1法,共有5×1=5法.
②A→DE→B,从A到D,最短的路程需要向下走2次,向右走3次,即从5次中任取2次向下,剩下3次向右,故有C52=10种,
从E到B,最短的路程需要向下走3次,向右走1次,即从4次中任取3次向下,剩下1次向右,故有C43=4种,
∴从A→DE→B共有10×4=40法,
∴从A到B的短程线总共5+40=45种走法.
故答案为:45.
点评 对于复杂一点的计数问题,有时分类以后,每类方法并不都是一步完成的,必须在分类后又分步,综合利用两个原理解决,即类中有步,步中有类.

练习册系列答案
相关题目
8.为了解某班学生喜欢打篮球是否与性别有关,对本班50人进行了问卷调查,得到如下2×2列联表:
经计算得到随机变量K2的观测值为8.333,则有99.5%的把握认为喜爱打篮球与性别有关(临界值参考表如下).
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥K0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
9.已知集合A={x|(x-1)(x-4)≤0},$B=\{x|\frac{x-5}{x-2}≤0\}$,则A∩B=( )
| A. | {x|1≤x≤2} | B. | {x|1≤x<2} | C. | {x|2≤x≤4} | D. | {x|2<x≤4} |
10.2016年济南地铁正式开工建设,地铁时代的到来能否缓解济南的交通拥堵状况呢?某社团进行社会调查,得到的数据如表:
则下列结论正确的是( )
附:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
| 男性市民 | 女性市民 | |
| 认为能缓解交通拥堵 | 48 | 30 |
| 认为不能缓解交通拥堵 | 12 | 20 |
附:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
| P(x2≥k) | 0.05 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 6.635 | 7.879 | 10.828 |
| A. | 有95%的把握认为“对能否缓解交通拥堵的认识与性别有关” | |
| B. | 有95%的把握认为“对能否缓解交通拥堵的认识与性别无关” | |
| C. | 有99%的把握认为“对能否缓解交通拥堵的认识与性别有关” | |
| D. | 有99%的把握认为“对能否缓解交通拥堵的认识与性别无关” |
7.已知平面α⊥平面β,则“直线m⊥平面α”是“直线m∥平面β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
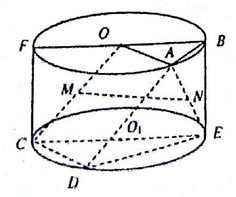 如图,矩形FCEB是圆柱OO1的轴截面,且FC=1,FB=2,点A、D分别在上下底面圆周上,且在面FCEB的同侧,△OAB是等边三角形,∠ECD=60°,M、N分别是OC、AE的中点.
如图,矩形FCEB是圆柱OO1的轴截面,且FC=1,FB=2,点A、D分别在上下底面圆周上,且在面FCEB的同侧,△OAB是等边三角形,∠ECD=60°,M、N分别是OC、AE的中点.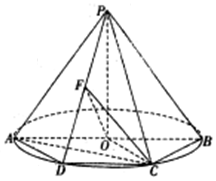 如图,AB是圆O的直径,点C,D是圆O上异于A,B的点,CD∥AB,F为PD中点,PO⊥垂直于圆O所在的平面,∠ABC=60°.
如图,AB是圆O的直径,点C,D是圆O上异于A,B的点,CD∥AB,F为PD中点,PO⊥垂直于圆O所在的平面,∠ABC=60°.