题目内容
3.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x+y-3≤0}\\{x-2y-3≤0}\end{array}\right.$,则目标函数z=2x+y的最小值为( )| A. | 6 | B. | 4 | C. | 2 | D. | 1 |
分析 由约束条件作出可行域,数形结合得到最优解,求出最优解的坐标,代入目标函数得答案.
解答 解:由变量x,y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x+y-3≤0}\\{x-2y-3≤0}\end{array}\right.$,作出可行域如图,
化目标函数z=2x+y为y=-2x+z,
由图可知,当直线y=-2x+z过A(1,-1)时直线在y轴上的截距最小,z最小,为2×1-1=1.
故选:D.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
14.设集合A={x|x<2},B={y|y=2x-1},则A∩B=( )
| A. | (-∞,3) | B. | [2,3) | C. | (-∞,2) | D. | (-1,2) |
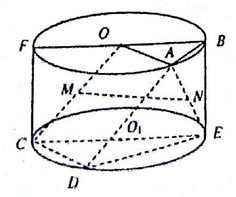 如图,矩形FCEB是圆柱OO1的轴截面,且FC=1,FB=2,点A、D分别在上下底面圆周上,且在面FCEB的同侧,△OAB是等边三角形,∠ECD=60°,M、N分别是OC、AE的中点.
如图,矩形FCEB是圆柱OO1的轴截面,且FC=1,FB=2,点A、D分别在上下底面圆周上,且在面FCEB的同侧,△OAB是等边三角形,∠ECD=60°,M、N分别是OC、AE的中点. ,且
,且
 则
则 等于( )
等于( ) B.
B.
 D.
D.
