题目内容
8．
已知全集U=R，集合A={x|x2-2x≤0}，B={y|y=sinx，x∈R}，则图中阴影部分表示的集合为（ ）| A． | [-1，2] | B． | [-1，0）∪（1，2] | C． | [0，1] | D． | （-∞，-1）∪（2，+∞） |
分析 根据阴影部分对应的集合为∁U（A∩B）∩（A∪B），然后根据集合的基本运算进行求解即可．
解答 解：A={x|x2-2x≤0}={x|0≤x≤2}，B={y|y=sinx，x∈R}={y|-1≤y≤1}，
由题意可知阴影部分对应的集合为∁U（A∩B）∩（A∪B），
∴A∩B={x|0≤x≤1}，A∪B={x|-1≤x≤2}，
即∁U（A∩B）={x|x＜0或x＞1}，
∴∁U（A∩B）∩（A∪B）={x|-1≤x＜0或1＜x≤2}，
故选：B
点评 本题主要考查集合的基本运算，利用阴影部分表示出集合关系是解决本题的关键．
练习册系列答案
相关题目
18．集合A={2，4，6，8，10}，B={1，3，5，7，9}，在A中任取一元素m和在B中任取一元素n，则所取两数m＞n的概率是（ ）
| A． | 0.4 | B． | 0.5 | C． | 0.6 | D． | 0.7 |
19．复数$z=\frac{{（{1-i}）（{4-i}）}}{1+i}$的共轭复数是（ ）
| A． | -4i | B． | -4 | C． | 4i | D． | -1+4i |
16．设G是△ABC的重心，点E是AG的中点，若$\overrightarrow{BA}$•$\overrightarrow{CA}$=4，$\overrightarrow{BG}$•$\overrightarrow{CG}$=-1，则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是（ ）
| A． | -$\frac{7}{8}$ | B． | $\frac{5}{8}$ | C． | $\frac{7}{8}$ | D． | $\frac{13}{8}$ |
3．设i为虚数单位，（-3+4i）2=a+bi（a，b∈R），则下列判断正确的是（ ）
| A． | |a+bi|=5 | B． | a+b=1 | C． | a-b=-17 | D． | ab=168 |
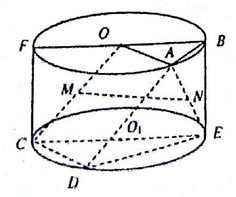如图，矩形FCEB是圆柱OO1的轴截面，且FC=1，FB=2，点A、D分别在上下底面圆周上，且在面FCEB的同侧，△OAB是等边三角形，∠ECD=60°，M、N分别是OC、AE的中点．