题目内容
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1(a>0)的一条渐近线与直线2x+y-3=0垂直,则该双曲线的离心率是$\frac{\sqrt{5}}{2}$.分析 根据题意,由双曲线的方程计算可得其渐近线方程为y=±$\frac{x}{a}$,进而由直线垂直的性质分析可得有$\frac{1}{a}$=$\frac{1}{2}$,解可得a的值,由双曲线的几何性质可得c的值,进而有双曲线的离心率公式计算可得答案.
解答 解:根据题意,双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-y2=1,则其渐近线方程为y=±$\frac{x}{a}$,
又由双曲线的一条渐近线与直线2x+y-3=0即y=-2x+3垂直,
则有$\frac{1}{a}$=$\frac{1}{2}$,
即a=2,
又由b=1,则c=$\sqrt{4+1}$=$\sqrt{5}$,
则双曲线的离心率e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$;
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查双曲线的几何性质,关键掌握双曲线的渐近线方程.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
9.已知集合A={x|(x-1)(x-4)≤0},$B=\{x|\frac{x-5}{x-2}≤0\}$,则A∩B=( )
| A. | {x|1≤x≤2} | B. | {x|1≤x<2} | C. | {x|2≤x≤4} | D. | {x|2<x≤4} |
16.设G是△ABC的重心,点E是AG的中点,若$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BG}$•$\overrightarrow{CG}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
| A. | -$\frac{7}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{13}{8}$ |
10.2016年济南地铁正式开工建设,地铁时代的到来能否缓解济南的交通拥堵状况呢?某社团进行社会调查,得到的数据如表:
则下列结论正确的是( )
附:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
| 男性市民 | 女性市民 | |
| 认为能缓解交通拥堵 | 48 | 30 |
| 认为不能缓解交通拥堵 | 12 | 20 |
附:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
| P(x2≥k) | 0.05 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 6.635 | 7.879 | 10.828 |
| A. | 有95%的把握认为“对能否缓解交通拥堵的认识与性别有关” | |
| B. | 有95%的把握认为“对能否缓解交通拥堵的认识与性别无关” | |
| C. | 有99%的把握认为“对能否缓解交通拥堵的认识与性别有关” | |
| D. | 有99%的把握认为“对能否缓解交通拥堵的认识与性别无关” |
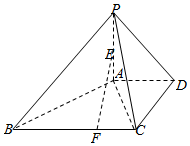 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,BC=4,AD=DC=2,E为PA的中点,F为线段BC上一点,且CF=1.
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,BC=4,AD=DC=2,E为PA的中点,F为线段BC上一点,且CF=1.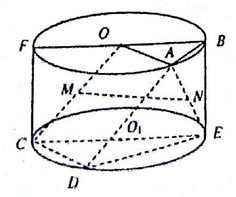 如图,矩形FCEB是圆柱OO1的轴截面,且FC=1,FB=2,点A、D分别在上下底面圆周上,且在面FCEB的同侧,△OAB是等边三角形,∠ECD=60°,M、N分别是OC、AE的中点.
如图,矩形FCEB是圆柱OO1的轴截面,且FC=1,FB=2,点A、D分别在上下底面圆周上,且在面FCEB的同侧,△OAB是等边三角形,∠ECD=60°,M、N分别是OC、AE的中点.