题目内容
5.在平面直角坐标系xOy中,动点S到点F(1,0)的距离与到直线x=2的距离的比值为$\frac{{\sqrt{2}}}{2}$.(Ⅰ)求动点S的轨迹E的方程;
(Ⅱ)设点P是x轴上的一个动点,过P作斜率为$\frac{{\sqrt{2}}}{2}$的直线l交轨迹E于A,B两点,求证:|PA|2+|PB|2为定值.
分析 (I)根据椭圆第二定义列方程组解出;
(II)求出直线的参数方程,代入椭圆方程化简,根据参数的几何意义和根与系数的关系计算:|PA|2+|PB|2.
解答 解:(I)由椭圆的定义可知动点S的轨迹为以F为右焦点,以直线x=2为准线的椭圆,
设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,则$\left\{\begin{array}{l}{c=1}\\{\frac{{a}^{2}}{c}=2}\\{{a}^{2}-{b}^{2}={c}^{2}}\end{array}\right.$,解得a2=2,b2=1,
∴轨迹E的方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(II)证明:设直线l的倾斜角为α,则tanα=$\frac{\sqrt{2}}{2}$,∴sinα=$\frac{\sqrt{3}}{3}$,cosα=$\frac{\sqrt{6}}{3}$.
设P(x0,0),则直线l的参数方程为$\left\{\begin{array}{l}{x={x}_{0}+\frac{\sqrt{6}}{3}t}\\{y=\frac{\sqrt{3}}{3}t}\end{array}\right.$,
代入为$\frac{{x}^{2}}{2}+{y}^{2}$=1得4t2+2$\sqrt{6}$x0t+3(x02-2)=0,
设方程两根为t1,t2,则t1+t2=-$\frac{\sqrt{6}{x}_{0}}{2}$,t1t2=$\frac{3({{x}_{0}}^{2}-2)}{4}$,
∴|PA|2+|PB|2=t12+t22=(t1+t2)2-2t1t2=$\frac{3}{2}$x02-$\frac{3}{2}$(x02-2)=3.
∴:|PA|2+|PB|2为定值3.
点评 本题考查了椭圆的定义和性质,直线与椭圆的位置关系,属于中档题.

| A. | -$\frac{7}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{13}{8}$ |
| 男性市民 | 女性市民 | |
| 认为能缓解交通拥堵 | 48 | 30 |
| 认为不能缓解交通拥堵 | 12 | 20 |
附:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
| P(x2≥k) | 0.05 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 6.635 | 7.879 | 10.828 |
| A. | 有95%的把握认为“对能否缓解交通拥堵的认识与性别有关” | |
| B. | 有95%的把握认为“对能否缓解交通拥堵的认识与性别无关” | |
| C. | 有99%的把握认为“对能否缓解交通拥堵的认识与性别有关” | |
| D. | 有99%的把握认为“对能否缓解交通拥堵的认识与性别无关” |
| A. | (-∞,3) | B. | [2,3) | C. | (-∞,2) | D. | (-1,2) |
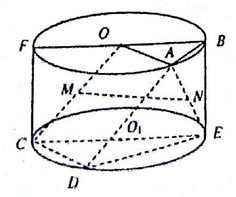 如图,矩形FCEB是圆柱OO1的轴截面,且FC=1,FB=2,点A、D分别在上下底面圆周上,且在面FCEB的同侧,△OAB是等边三角形,∠ECD=60°,M、N分别是OC、AE的中点.
如图,矩形FCEB是圆柱OO1的轴截面,且FC=1,FB=2,点A、D分别在上下底面圆周上,且在面FCEB的同侧,△OAB是等边三角形,∠ECD=60°,M、N分别是OC、AE的中点.