题目内容
已知函数f(x)=2
sinxcosx-3sin2x-cos2x+3.
(1)当x∈[0,
]时,求f(x)的值域;
(2)若△ABC的内角A,B,C的对边分别为a,b,c,且满足
=
,
=2+2cos(A+C),求f(B)的值.
| 3 |
(1)当x∈[0,
| π |
| 2 |
(2)若△ABC的内角A,B,C的对边分别为a,b,c,且满足
| b |
| a |
| 3 |
| sin(2A+C) |
| sinA |
考点:正弦定理,三角函数中的恒等变换应用
专题:三角函数的求值,解三角形
分析:(1)由三角函数公式化简可得f(x)=2sin(2x+
)+1,由x的范围结合三角函数的运算可得;(2)由三角函数公式和已知数据可得c=2a,b=
a,代入余弦定理可得cosA=
,可得A=30°,进而可得C=90°,B=60°,代入可得其值.
| π |
| 6 |
| 3 |
| ||
| 2 |
解答:
解:(1)∵f(x)=2
sinxcosx-3sin2x-cos2x+3
=
sin2x-3•
-
+3
=
sin2x-cos2x+1=2sin(2x+
)+1,
∵x∈[0,
],∴2x+
∈[
,
],
∴sin(2x+
)∈[-
,1],
∴f(x)=2sin(2x+
)+1∈[0,3];
(2)∵
=2+2cos(A+C),
∴sin(2A+C)=2sinA+2sinAcos(A+C),
∴sinAcos(A+C)+cosAsin(A+C)=2sinA+2sinAcos(A+C),
∴-sinAcos(A+C)+cosAsin(A+C)=2sinA,即sinC=2sinA,
由正弦定理可得c=2a,又由
=
可得b=
a,
由余弦定理可得cosA=
=
=
,
∴A=30°,由正弦定理可得sinC=2sinA=1,C=90°,
由三角形的内角和可得B=60°,
∴f(B)=f(60°)=2
| 3 |
=
| 3 |
| 1-cos2x |
| 2 |
| 1+cos2x |
| 2 |
=
| 3 |
| π |
| 6 |
∵x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴sin(2x+
| π |
| 6 |
| 1 |
| 2 |
∴f(x)=2sin(2x+
| π |
| 6 |
(2)∵
| sin(2A+C) |
| sinA |
∴sin(2A+C)=2sinA+2sinAcos(A+C),
∴sinAcos(A+C)+cosAsin(A+C)=2sinA+2sinAcos(A+C),
∴-sinAcos(A+C)+cosAsin(A+C)=2sinA,即sinC=2sinA,
由正弦定理可得c=2a,又由
| b |
| a |
| 3 |
| 3 |
由余弦定理可得cosA=
| b2+c2-a2 |
| 2bc |
| 3a2+4a2-a2 | ||
2•
|
| ||
| 2 |
∴A=30°,由正弦定理可得sinC=2sinA=1,C=90°,
由三角形的内角和可得B=60°,
∴f(B)=f(60°)=2
点评:本题考查三角形的正余弦定理,涉及三角函数的公式,属中档题.

练习册系列答案
相关题目
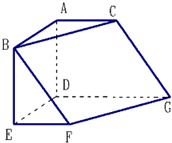 在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,四边形 DEFG 是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.
在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,四边形 DEFG 是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.