题目内容

等边△ABC的边长为1，延长CB到点D，使BD=2，连结AD，则sin∠BAD=
 
．
考点：余弦定理,同角三角函数基本关系的运用
专题：三角函数的求值
分析：根据题意画出图形，如图所示，在三角形ACD中，由AC，CD，以及cosC的值，利用余弦定理求出AD的长，在三角形ABD中，由余弦定理表示出cos∠BAD，将三边长代入求出cos∠BAD的值，再利用同角三角函数间基本关系求出sin∠BAD的值即可．
解答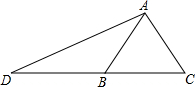： 解：根据题意画出图形，如图所示，
在△ADC中，AC=1，CD=BC+BD=1+2=3，cosC=cos60°=
1
2
，
∴由余弦定理得：AD2=AC2+CD2-2AC•CD•cosC=1+9-3=7，即AD=
7
，
在△ABD中，AD=
7
，BD=2，AB=1，
∴cos∠BAD=
AD2+AB2-BD2
2AD•AB
=
7+1-4
2
7
=
2
7
7
，
则sin∠BAD=
1-(
2
7
7
)2
=
21
7
．
故答案为：
21
7
点评：此题考查了余弦定理，以及同角三角函数间基本关系的运用，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
已知函数f（x）=ax2-1nx，x∈（0，e]，其中e是自然对数的底数，a∈R．
（1）当a=1时，求函数f（x）的单调区间与极值；
（2）对于任意的x∈（0，e]，f（x）≥3恒成立，求实数a的取值范围．
已知定点A（1，0），B为x轴负半轴上的动点，以AB为边作菱形ABCD，使其两对角线的交点H恰好落在y轴上．
（1）求动点D的轨迹E的方程；
（2）若四边形MPNQ的四个顶点都在曲线E上，M、N关于x轴对称，曲线E在点M处的切线为l，且PQ∥l．
①证明：直线PN与QN的斜率之和为定值；
②当点M的横坐标为
3
4
，纵坐标大于0，∠PNQ=60°，求四边形MPNQ的面积．
已知函数f（x）=2
3
sinxcosx-3sin2x-cos2x+3．
（1）当x∈[0，
π
2
]时，求f（x）的值域；
（2）若△ABC的内角A，B，C的对边分别为a，b，c，且满足
b
a
=
3
，
sin(2A+C)
sinA
=2+2cos（A+C），求f（B）的值．
已知函数f（x）=x3-ax2-x；
（1）若f（x）在(-
1
3
，1)上单调递减，在（1，+∞）上单调递增，求实数a的值；
（2）当a=
1
2
时，求证：当x＞0时，f(x)≥x-
3
2
．
已知函数f（x）=
1
x-m
，若存在α∈（0，
π
2
），使f（sinα）+f（cosα）=0，则实数m的取值范围是
 
．
设变量x、y满足约束条件
x-y+2≥0
x-5y+10≤0
x+y-8≤0
，则目标函数z=3x-4y的最大值为
 
．
十二届全国人大二次会议上，李克强总理提出“以雾霾频发的特大城市和区域为重点，以细颗粒物PM2.5和可吸入颗粒物PM10为突破口…”治理污染，“要像对贫困宣战一样，坚决向污染宣战”，其中总理提到的“PM2.5”是指大气中直径小于或等于2.5微米的颗粒物，也称为人肺颗粒物．根据现行国家标准GB3095-2012，PM2.5日均值在35微克/立方米-75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．从某市2013年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本，监测值频数如茎叶图所示（十位为茎，个位为叶）：
（1）求空气质量为超标的数据的平均数与方差；
（2）在空气质量为二级的数据中任取2个，求这2个数据的和小于100的概率；
（3）以这12天的PM2.5日均值来估计2013年的空气质量状况，则2013年（按366天算）中平均有多少天的空气质量达到一级或二级．
关于函数f（x）=|2sinx+m|（m为常数且m∈R），有下列结论：
①若m=0，则函数f（x）的最小正周期为π；
②如果函数f（x）的最小正周期为2π，则m＞0；
③函数f（x）图象的对称轴方程式x=kπ+
π
2
（k∈Z）；
④存在常数m、k使得函数g（x）=f（x）-k（x＞0）的零点从小到大排列成公差为2π的等差数列；
⑤存在唯一的一组常数m、k，使得函数g（x）=f（x）-k（x＞0）的零点从小到大排列成公差为π的等差数列；
其中正确结论的序号为
 
（把你认为正确结论的序号都填上）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网