题目内容
某次中俄军演中,中方参加演习的有4艘军舰、3架飞机;俄方有5艘军舰、2架飞机.从中俄两方中各选出2个单位(1艘军舰或1架飞机都作为一个单位,所有的军舰两两不同,所有的飞机两两不同),则选出的四个单位中恰有一架飞机的不同选法共有( )
| A、180种 | B、160种 |
| C、120种 | D、38种 |
考点:计数原理的应用
专题:
分析:根据题意,分从中方选一架飞机、从俄方选一架飞机2种情况讨论,分别求出每种情况下的选法数目,由分类加法原理计算可得答案.
解答:
解:根据题意,分2种情况讨论:
①、若从中方选一架飞机,则选法有
=120种;
②、若从俄方选一架飞机,则选法有
=60种.
则不同选法共120+60=180种.
故选A.
①、若从中方选一架飞机,则选法有
| C | 1 4 |
| C | 1 3 |
| C | 2 5 |
②、若从俄方选一架飞机,则选法有
| C | 1 5 |
| C | 1 2 |
| C | 2 4 |
则不同选法共120+60=180种.
故选A.
点评:本题考查计数原理的运用,涉及组合公式的应用,注意需要根据题意进行分类讨论.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
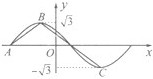 如图为函数f(x)=
如图为函数f(x)=| 3 |
| AB |
| BC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a,b为实数,则“2a>2b”是“a2>b2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既充分也不必要条件 |
点P在边长为1的正方形ABCD内部运动,则点P到此正方形中心点的距离均不超过
的概率为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、π |
要得到函数y=cos(2x-
)的图象,只需将函数y=sin(2x)的图象( )
| π |
| 3 |
A、左移
| ||
B、右移
| ||
C、左移
| ||
D、右移
|
某工厂安排甲、乙两种产品的生产,已知工厂生产每吨甲、乙两种产品所需要的原材料A、B、C的数量和一周内可用资源数量如下表所示:
如果甲产品每吨的利润为300元,乙产品每吨的利润为200元,此处不考虑市场的有限性,则工厂每周要获得最大利润,最科学的安排生产方式是( )
| 原材料 | 甲(吨) | 乙(吨) | 资源数量(吨) |
| A | 1 | 1 | 50 |
| B | 4 | 0 | 160 |
| C | 2 | 5 | 200 |
| A、每周生产甲产品40吨,不生产乙产品 | ||||
| B、每周不生产甲产品,生产乙产品40吨 | ||||
C、每周生产甲产品
| ||||
| D、每周生产甲产品40吨,生产乙产品10吨 |