题目内容
已知函数f（x）=2sin（
x+φ）（x∈R，0＜φ＜
）的图象过点M（
，
）．
（1）求φ的值；
（2）设α，β∈[0，
]，f（3α+π）=
，f（3β+
）=-
，求sin（α-β）的值．
| 1 |
| 3 |
| π |
| 2 |
| π |
| 2 |
| 3 |
（1）求φ的值；
（2）设α，β∈[0，
| π |
| 2 |
| 10 |
| 13 |
| 5π |
| 2 |
| 6 |
| 5 |
考点：两角和与差的正弦函数,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的求值
分析：（1）依题意求得sin（
+φ）=
，结合0＜φ＜
求得φ的值．
（2）由条件求得cosα=
，sinβ=
．根据α，β∈[0，
]，利用同角三角函数的基本关系求得inα 和cosβ 的值，从而求得 sin（α-β）=sinαcosβ-cosαsinβ 的值．
| π |
| 6 |
| ||
| 2 |
| π |
| 2 |
（2）由条件求得cosα=
| 5 |
| 13 |
| 3 |
| 5 |
| π |
| 2 |
解答：
解：（1）依题意得2sin（
+φ）=
，即sin（
+φ）=
，
∵0＜φ＜
，∴
＜φ+
＜
，∴φ+
=
，φ=
．
（2）∵f（3α+π）=2sin（α+
）=2cosα=
，∴cosα=
．
∵f（3β+
）=2sin（β+π）=-2sinβ=-
，∴sinβ=
．
∵α，β∈[0，
]，∴sinα=
=
，cosβ=
=
，
∴sin（α-β）=sinαcosβ-cosαsinβ=
×
-
×
=
．
| π |
| 6 |
| 3 |
| π |
| 6 |
| ||
| 2 |
∵0＜φ＜
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
（2）∵f（3α+π）=2sin（α+
| π |
| 2 |
| 10 |
| 13 |
| 5 |
| 13 |
∵f（3β+
| 5π |
| 2 |
| 6 |
| 5 |
| 3 |
| 5 |
∵α，β∈[0，
| π |
| 2 |
| 1-cos2α |
| 12 |
| 13 |
| 1-sin2β |
| 4 |
| 5 |
∴sin（α-β）=sinαcosβ-cosαsinβ=
| 12 |
| 13 |
| 4 |
| 5 |
| 5 |
| 13 |
| 3 |
| 5 |
| 33 |
| 65 |
点评：本题主要考查同角三角函数的基本关系、两角和的正弦公式、诱导公公式的应用，根据三角函数的值求角，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
某工厂安排甲、乙两种产品的生产，已知工厂生产每吨甲、乙两种产品所需要的原材料A、B、C的数量和一周内可用资源数量如下表所示：
如果甲产品每吨的利润为300元，乙产品每吨的利润为200元，此处不考虑市场的有限性，则工厂每周要获得最大利润，最科学的安排生产方式是（ ）
| 原材料 | 甲（吨） | 乙（吨） | 资源数量（吨） |
| A | 1 | 1 | 50 |
| B | 4 | 0 | 160 |
| C | 2 | 5 | 200 |
| A、每周生产甲产品40吨，不生产乙产品 | ||||
| B、每周不生产甲产品，生产乙产品40吨 | ||||
C、每周生产甲产品
| ||||
| D、每周生产甲产品40吨，生产乙产品10吨 |
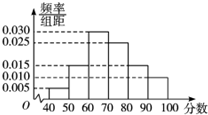某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分为6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）加以统计，得到如图所示的频率分布直方图，已知高一年级共有600名，据此估计，该模块测试成绩的平均分为