题目内容
设函数f(x)=lnx-ax,g(x)=ex-ax,其中a为实数.
(1)若f(x)在(2,+∞)上是单调减函数,且g(x)在(2,+∞)上有最小值,求a的取值范围;
(2)若g(x)在(0,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论.
(1)若f(x)在(2,+∞)上是单调减函数,且g(x)在(2,+∞)上有最小值,求a的取值范围;
(2)若g(x)在(0,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)求导数,利用函数的单调性与g(x)在(2,+∞)上有最小值,即可求a的取值范围;
(2)先确定a≤1,令f(x)=0,a=
,设h(x)=
,求导数,分类讨论,确定函数的单调性,结合函数的图象,即可求f(x)的零点个数.
(2)先确定a≤1,令f(x)=0,a=
| lnx |
| x |
| lnx |
| x |
解答:
解:(1)f(x)在(2,+∞)上是单调减函数,
则当x∈(2,+∞),f′(x)=
-a≤0恒成立,a≥
恒成立,
∴a≥(
)max=
.
令g′(x)=ex-a=0,得x=ln a.
当x<ln a时,g′(x)<0;当x>ln a时,g′(x)>0.
又g(x)在(2,+∞)上有最小值,
所以ln a>2,即a>e2.
综上,有a∈(e2,+∞).
(2)当x∈(0,+∞),g′(x)=ex-a≥0恒成立,a≤(ex)min,∴a≤1
令f(x)=0,a=
,设h(x)=
,h/(x)=
(x>0),
令h′(x)=0,x=e
当x∈(0,e),h′(x)>0,h(x)在(0,e)上单调递增
当x∈(e,+∞),h′(x)<0,h(x)在(e,+∞)上单调递减,
∴h(x)的最大值为h(e)=
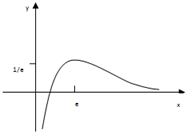
h(x)的大致图象如图所示:
当
<a≤1时无零点,0<a<
时,两个零点,a≤0,a=
时一个零点.
则当x∈(2,+∞),f′(x)=
| 1 |
| x |
| 1 |
| x |
∴a≥(
| 1 |
| x |
| 1 |
| 2 |
令g′(x)=ex-a=0,得x=ln a.
当x<ln a时,g′(x)<0;当x>ln a时,g′(x)>0.
又g(x)在(2,+∞)上有最小值,
所以ln a>2,即a>e2.
综上,有a∈(e2,+∞).
(2)当x∈(0,+∞),g′(x)=ex-a≥0恒成立,a≤(ex)min,∴a≤1
令f(x)=0,a=
| lnx |
| x |
| lnx |
| x |
| 1-lnx |
| x2 |
令h′(x)=0,x=e
当x∈(0,e),h′(x)>0,h(x)在(0,e)上单调递增
当x∈(e,+∞),h′(x)<0,h(x)在(e,+∞)上单调递减,
∴h(x)的最大值为h(e)=
| 1 |
| e |
h(x)的大致图象如图所示:

当
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
点评:本题考查导数知识的综合运用,考查函数的单调性与最值,考查函数的零点,考查分类讨论、数形结合的数学思想,正确运用导数是关键.

练习册系列答案
相关题目
点P在边长为1的正方形ABCD内部运动,则点P到此正方形中心点的距离均不超过
的概率为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、π |