题目内容
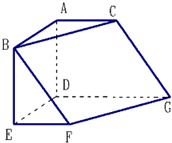 在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,四边形 DEFG 是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.
在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,四边形 DEFG 是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.(1)求证:FG⊥面ADF;
(2)求二面角F-GC-D的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(1)连接DF,证明FG⊥DF,AD⊥FG,利用线面垂直的判定定理,即可证明FG⊥面ADF;
(2)建立空间直角坐标系,求出平面FGC的法向量、平面GCD的一个法向量,利用向量的夹角公式,即可求二面角F-GC-D的余弦值
(2)建立空间直角坐标系,求出平面FGC的法向量、平面GCD的一个法向量,利用向量的夹角公式,即可求二面角F-GC-D的余弦值
解答:
 (1)证明:连接DF,则DF=1,FG=BC=
(1)证明:连接DF,则DF=1,FG=BC=
=
,
∵DG=2,
∴DF2+FG2=DG2,
∴FG⊥DF,
∵四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,
∴AD⊥DE,AD⊥DG,
∵DE∩DG=D,
∴AD⊥四边形DEFG,
∴AD⊥FG,
∵AD∩DF=D,
∴FG⊥面ADF;
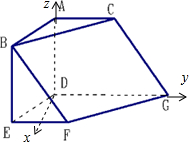
(2)解:建立如图所示的坐标系,则F(
,
,0),G(0,2,0),C(0,1,1),
∴
=(-
,
,0),
=(0,-1,1),
设平面FGC的法向量为
=(x,y,z),则
,
取
=(
,1,1),
∵平面GCD的一个法向量为
=(
,0,0),
∴二面角F-GC-D的余弦值为
=
.
 (1)证明:连接DF,则DF=1,FG=BC=
(1)证明:连接DF,则DF=1,FG=BC=| 1+1-2•1•1•cos120° |
| 3 |
∵DG=2,
∴DF2+FG2=DG2,
∴FG⊥DF,
∵四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,
∴AD⊥DE,AD⊥DG,
∵DE∩DG=D,
∴AD⊥四边形DEFG,
∴AD⊥FG,
∵AD∩DF=D,
∴FG⊥面ADF;
(2)解:建立如图所示的坐标系,则F(
| ||
| 2 |
| 1 |
| 2 |
∴
| FG |
| ||
| 2 |
| 3 |
| 2 |
| GC |
设平面FGC的法向量为
| n |
|
取
| n |
| 3 |
∵平面GCD的一个法向量为
| m |
| ||
| 2 |
∴二面角F-GC-D的余弦值为
| ||||||
|
| ||
| 5 |
点评:本题以不规则几何体为载体,考查空间线面关系的判断与证明,空间角的计算,坚持向量法与公理化法的“双轨”处理模式,在复习备考时应引起高度注意.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知a,b为实数,则“2a>2b”是“a2>b2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既充分也不必要条件 |
 十二届全国人大二次会议上,李克强总理提出“以雾霾频发的特大城市和区域为重点,以细颗粒物PM2.5和可吸入颗粒物PM10为突破口…”治理污染,“要像对贫困宣战一样,坚决向污染宣战”,其中总理提到的“PM2.5”是指大气中直径小于或等于2.5微米的颗粒物,也称为人肺颗粒物.根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米-75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某市2013年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本,监测值频数如茎叶图所示(十位为茎,个位为叶):
十二届全国人大二次会议上,李克强总理提出“以雾霾频发的特大城市和区域为重点,以细颗粒物PM2.5和可吸入颗粒物PM10为突破口…”治理污染,“要像对贫困宣战一样,坚决向污染宣战”,其中总理提到的“PM2.5”是指大气中直径小于或等于2.5微米的颗粒物,也称为人肺颗粒物.根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米-75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某市2013年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本,监测值频数如茎叶图所示(十位为茎,个位为叶):