题目内容
4.若曲线f(x,y)=0上两个不同的点处的切线重合,则称这条切线为曲线f(x,y)=0的自公切线,则下列方程对应的曲线中存在自公切线的为( )①y=x2-|x|+1; ②y=sinx-4cosx; ③$y=x+\frac{1}{x}$; ④$|x|+1=\sqrt{4-{y^2}}$.
| A. | ②③ | B. | ①② | C. | ①②④ | D. | ①②③ |
分析 化简函数的解析式,结合函数的图象的特征,判断此函数是否有自公切线.
解答 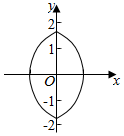 解:①、y=x2-|x|+1=$\left\{\begin{array}{l}{(x-\frac{1}{2})^{2}+\frac{3}{4},x≥0}\\{(x+\frac{1}{2})^{2}+\frac{3}{4},x<0}\end{array}\right.$,在x=$\frac{1}{2}$和x=-$\frac{1}{2}$ 处的切线都是y=$\frac{3}{4}$,故有自公切线.
解:①、y=x2-|x|+1=$\left\{\begin{array}{l}{(x-\frac{1}{2})^{2}+\frac{3}{4},x≥0}\\{(x+\frac{1}{2})^{2}+\frac{3}{4},x<0}\end{array}\right.$,在x=$\frac{1}{2}$和x=-$\frac{1}{2}$ 处的切线都是y=$\frac{3}{4}$,故有自公切线.
②、y=3sinx+4cosx=5sin(x+φ),cosφ=$\frac{3}{5}$,sinφ=$\frac{4}{5}$,
此函数是周期函数,过图象的最高点的切线都重合,故此函数有自公切线.
③、$y=x+\frac{1}{x}$为对勾函数,分别位于一三象限,图象关于原点对称且导数为
y′=1-$\frac{1}{{x}^{2}}$,在(-∞,-1),(1,+∞)递增,(-1,0),(0,1)递减,存在平行的切线,不存在自公切线;
④、由于|x|+1=$\sqrt{4-{y}^{2}}$,即 x2+2|x|+y2-3=0,结合图象可得,此曲线没有自公切线.
故选:B.
点评 本题考查函数的自公切线的定义,函数图象的特征,准确判断一个函数是否有自公切线,是解题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知数列{an}的前n项和Sn=an2+bn(a,b∈R)且a2=3,a6=11,则S7等于( )
| A. | 13 | B. | 35 | C. | 49 | D. | 63 |
15.已知抛物线x2=2y的焦点与椭圆$\frac{{y}^{2}}{m}$+$\frac{{x}^{2}}{2}$=1的一个焦点重合,则m=( )
| A. | $\frac{9}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{2}$ |
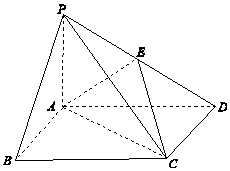 四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.