题目内容
14.定义在(-1,1)上的函数f(x)满足:$f(x)-f(y)=f({\frac{x-y}{1-xy}})$,当x∈(-1,0)时,有f(x)>0,且$f({-\frac{1}{2}})=1$.设$m=f({\frac{1}{5}})+f({\frac{1}{11}})+…+f({\frac{1}{{{n^2}+n-1}}}),\;\;n≥2,n∈{N^*}$,则实数m与-1的大小关系为( )| A. | m<-1 | B. | m=-1 | C. | m>-1 | D. | 不确定 |
分析 化简可得f(x)在(-1,1)为奇函数,由当x∈(-1,0)时,有f(x)>0,且$f({-\frac{1}{2}})=1$,从而可得在x∈(0,1)时f(x)<0,f($\frac{1}{2}$)=-1,f($\frac{1}{{n}^{2}+n-1}$)=f($\frac{1}{n(n+1)-1}$)=f($\frac{\frac{1}{n}-\frac{1}{n+1}}{1-\frac{1}{n(n+1)}}$)=f($\frac{1}{n}$)-f($\frac{1}{n+1}$),从而利用裂项求和法求得m与-1的大小.
解答 解:∵函数f(x)满足:$f(x)-f(y)=f({\frac{x-y}{1-xy}})$,
令x=y=0得f(0)=0;
令x=0得-f(y)=f(-y).
∴f(x)在(-1,1)为奇函数,
由当x∈(-1,0)时,有f(x)>0,且$f({-\frac{1}{2}})=1$,
则在x∈(0,1)时f(x)<0,f($\frac{1}{2}$)=-1,
∵f($\frac{1}{{n}^{2}+n-1}$)=f($\frac{1}{n(n+1)-1}$)=f($\frac{\frac{1}{n}-\frac{1}{n+1}}{1-\frac{1}{n(n+1)}}$)
=f($\frac{1}{n}$)-f($\frac{1}{n+1}$),
∴m=f($\frac{1}{5}$)+f($\frac{1}{11}$)+…+f($\frac{1}{{n}^{2}+n-1}$)
=[f($\frac{1}{2}$)-f($\frac{1}{3}$)]+[f($\frac{1}{3}$)-f($\frac{1}{4}$)]+…+[f($\frac{1}{n}$)-f($\frac{1}{n+1}$)]
=f($\frac{1}{2}$)-f($\frac{1}{n+1}$)=-1-f($\frac{1}{n+1}$)>-1,
即m>-1.
故选:C.
点评 本题考查了函数的奇偶性及运用,考查学生的化简运算能力及转化思想的应用,以及数列的求和方法:裂项相消求和,属于综合题.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案①y=x2-|x|+1; ②y=sinx-4cosx; ③$y=x+\frac{1}{x}$; ④$|x|+1=\sqrt{4-{y^2}}$.
| A. | ②③ | B. | ①② | C. | ①②④ | D. | ①②③ |
| A. | (0,+∞) | B. | (-∞,0)∪(3,+∞) | C. | (-∞,0)∪(1,+∞) | D. | (3,+∞) |
| A. | (1,3) | B. | (2,3) | C. | (1,2) | D. | (2,+∞) |
| A. | $\frac{1}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{1}{12}$ | D. | $\frac{4}{9}$ |
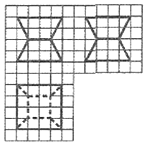 如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个棱长为4的正方体毛坯切削得到,则切削掉部分的体积与原毛坯体积的比值为( )
如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个棱长为4的正方体毛坯切削得到,则切削掉部分的体积与原毛坯体积的比值为( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |