题目内容
16.根据所给条件求直线的方程:(1)直线过点(-4,0),倾斜角的正弦值为$\frac{\sqrt{10}}{10}$;
(2)直线过点(-2,1),且到原点的距离为2.
分析 (1)由题设知,该直线的斜率存在,故可采用点斜式;
(2)分类讨论:斜率不存在和斜率存在两种情况.当斜率存在时,设其为k,则所求直线方程为y-1=k(x+2),即kx-y+(1+2k)=0.然后结合点到直线的距离公式求得k的值即可.
解答 解:(1)由题设知,该直线的斜率存在,故可采用点斜式.
设倾斜角为α,则sin α=$\frac{\sqrt{10}}{10}$(0<α<π),从而cos α=±$\frac{3\sqrt{10}}{10}$,则k=tan α=±$\frac{1}{3}$.
故所求直线方程为y=±$\frac{1}{3}$(x+4).即x+3y+4=0或x-3y+4=0;
(2)当斜率不存在时,所求直线方程为x+2=0;
当斜率存在时,设其为k,则所求直线方程为y-1=k(x+2),即kx-y+(1+2k)=0.
由点线距离公式,得$\frac{|1+2k|}{\sqrt{{k}^{2}+1}}$=2,
解得k=$\frac{3}{4}$.故所求直线方程为3x-4y+10=0.
综上知,所求直线方程为x+2=0或3x-4y+10=0.
点评 本题考查了直线方程问题,熟练掌握直线方程以及斜率问题是解题的关键,本题是一道基础题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
4.若曲线f(x,y)=0上两个不同的点处的切线重合,则称这条切线为曲线f(x,y)=0的自公切线,则下列方程对应的曲线中存在自公切线的为( )
①y=x2-|x|+1; ②y=sinx-4cosx; ③$y=x+\frac{1}{x}$; ④$|x|+1=\sqrt{4-{y^2}}$.
①y=x2-|x|+1; ②y=sinx-4cosx; ③$y=x+\frac{1}{x}$; ④$|x|+1=\sqrt{4-{y^2}}$.
| A. | ②③ | B. | ①② | C. | ①②④ | D. | ①②③ |
11.等差数列{an}中,已知a2+a10=16,则a4+a6+a8=( )
| A. | 16 | B. | 20 | C. | 24 | D. | 28 |
8.已知命题p:?x<0,x2>0,那么¬P是( )
| A. | ?x≥0,x2≤0 | B. | ?x≥0,x2≤0 | C. | ?x<0,x2≤0 | D. | ?x<0,x2≤0 |
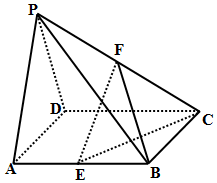 如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.