题目内容
15.已知抛物线x2=2y的焦点与椭圆$\frac{{y}^{2}}{m}$+$\frac{{x}^{2}}{2}$=1的一个焦点重合,则m=( )| A. | $\frac{9}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{2}$ |
分析 求出抛物线的焦点坐标,椭圆的焦点坐标重合,求解m即可.
解答 解:抛物线x2=2y的焦点(0,$\frac{1}{2}$)与椭圆$\frac{{y}^{2}}{m}$+$\frac{{x}^{2}}{2}$=1的一个焦点(0,$\sqrt{m-2}$)重合,可得$\sqrt{m-2}$=$\frac{1}{2}$,
解得m=$\frac{9}{4}$.
故选:A.
点评 本题考查椭圆的简单性质以及抛物线的简单性质的应用,考查计算能力.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
5.已知(x2+2x+3y)5的展开式中x5y2( )
| A. | 60 | B. | 180 | C. | 520 | D. | 540 |
10.若a1,a2,a3,…a20这20个数据的平均数为$\bar x$,方差为0.21,则a1,a2,a3,…a20,$\bar x$这21个数据的方差为( )
| A. | 0.19 | B. | 0.20 | C. | 0.21 | D. | 0.22 |
20.y=tan(πx+$\frac{π}{4}$)的对称中心为( )
| A. | ($\frac{(2k-1)π}{4}$,0),k∈Z | B. | $(\frac{2k-1}{2},0),k∈Z$ | C. | ($\frac{2k-1}{4}$,0),k∈Z | D. | ($\frac{(2k-1)π}{2}$,0),k∈Z |
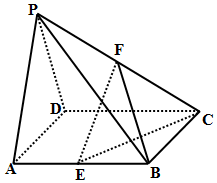 如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.