题目内容
13.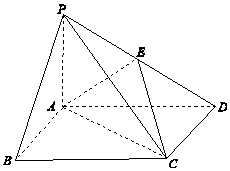 四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;
(2)设AP=1,AD=$\sqrt{3}$,三棱锥P-ABD的体积V=$\frac{{\sqrt{3}}}{4}$,求二面角D-AE-C的大小.
分析 (1)连结BD交AC于点O,连结EO,由已知可得EO∥PB,然后利用线面平行的判定可得PB∥平面AEC;
(2)由PA⊥平面ABCD,ABCD为矩形,可得AB,AD,AP两两垂直,以A为坐标原点,$\overrightarrow{AB}$ 的方向为x轴的正方向,建立空间直角坐标系A-xyz,再由三棱锥P-ABD的体积V=$\frac{{\sqrt{3}}}{4}$求得AB,得到A,D,B,E,C的坐标,然后求出平面ACE与平面DAE的法向量,由两法向量所成角的余弦值求得二面角D-AE-C的大小.
解答 (1)证明:连结BD交AC于点O,连结EO,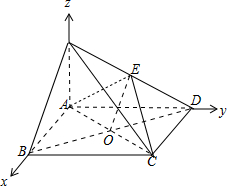
∵ABCD为矩形,∴O为BD的中点,
又E为的PD的中点,∴EO∥PB,
EO?平面AEC,PB?平面AEC,
∴PB∥平面AEC;
(2)解:∵PA⊥平面ABCD,ABCD为矩形,
∴AB,AD,AP两两垂直,
如图,以A为坐标原点,$\overrightarrow{AB}$ 的方向为x轴的正方向,
建立空间直角坐标系A-xyz,
∵AP=1,AD=$\sqrt{3}$,三棱锥P-ABD的体积V=$\frac{{\sqrt{3}}}{4}$,
∴三棱锥P-ABD的体积$V=\frac{1}{3}×\frac{1}{2}AB•AD•AP=\frac{\sqrt{3}}{4}$,得$AB=\frac{3}{2}$.
则A(0,0,0),D(0,$\sqrt{3}$,0),B($\frac{3}{2}$,0,0),E(0,$\frac{{\sqrt{3}}}{2}$,$\frac{1}{2}$),C ($\frac{3}{2}$,$\sqrt{3}$,0),
则$\overrightarrow{AE}$=(0,$\frac{{\sqrt{3}}}{2}$,$\frac{1}{2}$),$\overrightarrow{AC}$=($\frac{3}{2}$,$\sqrt{3}$,0)
设$\overrightarrow{m}=(x,y,z)$为平面ACE的法向量,
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AE}=0}\\{\overrightarrow{m}•\overrightarrow{AC}=0}\end{array}\right.$,即$\left\{\begin{array}{l}\frac{{\sqrt{3}}}{2}y+\frac{1}{2}z=0\\ \frac{3}{2}x+\sqrt{3}y=0\end{array}\right.$,令x=1,得$y=-\frac{{\sqrt{3}}}{2}$,$z=\frac{3}{2}$,则$\overrightarrow{m}$=(1,$-\frac{\sqrt{3}}{2}$,$\frac{3}{2}$),
又$\overrightarrow{n}=(1,0,0)$为平面DAE的法向量,
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{1}{\sqrt{1+\frac{3}{4}+\frac{9}{4}}}=\frac{1}{2}$,
如图可得二面角D-AE-C为锐角,∴二面角D-AE-C为$\frac{π}{3}$.
点评 本题考查直线与平面平行的判定,考查空间想象能力和思维能力,训练了利用空间向量求二面角的平面角,是中档题.

①y=x2-|x|+1; ②y=sinx-4cosx; ③$y=x+\frac{1}{x}$; ④$|x|+1=\sqrt{4-{y^2}}$.
| A. | ②③ | B. | ①② | C. | ①②④ | D. | ①②③ |
| A. | ?x≥0,x2≤0 | B. | ?x≥0,x2≤0 | C. | ?x<0,x2≤0 | D. | ?x<0,x2≤0 |
| A. | 8 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
| A. | (0,+∞) | B. | (-∞,0)∪(3,+∞) | C. | (-∞,0)∪(1,+∞) | D. | (3,+∞) |
| A. | $\frac{1}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{1}{12}$ | D. | $\frac{4}{9}$ |