题目内容
设不等式|x-
|+|x-
|<1的定义域为M,且a∈M,b∈M,试比较ab+1与a+b的大小.
| 1 |
| 4 |
| 3 |
| 4 |
考点:不等式比较大小
专题:不等式的解法及应用
分析:通过对x与
,
的大小关系分类讨论即可得出M,再通过作差即可比较出大小.
| 1 |
| 4 |
| 3 |
| 4 |
解答:
解:当x≤
时,原不等式化为
-x+
-x<1,化为x>0,∴0<x≤
.
当
<x<
时,原不等式化为x-
+
-x<1,化为
<1,∴
<x<
.
当
≤x时,原不等式化为x-
+x-
<1,化为x<1,∴
≤x<1.
综上可得M={x|0<x<1}.
∵a∈M,b∈M,∴0<a<1,0<b<1.
∴ab+1-(a+b)=(1-a)(1-b)>0.
∴ab+1>a+b.
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
当
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
当
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
综上可得M={x|0<x<1}.
∵a∈M,b∈M,∴0<a<1,0<b<1.
∴ab+1-(a+b)=(1-a)(1-b)>0.
∴ab+1>a+b.
点评:本题考查了含绝对值符号的不等式的解法、分类讨论的思想方法、作差法比较数的大小,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
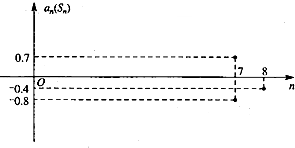 设等差数列{an}的前n项和为Sn,在同一个坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示,则( )
设等差数列{an}的前n项和为Sn,在同一个坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示,则( )| A、当n=4时,Sn取得最大值 |
| B、当n=3时,Sn取得最大值 |
| C、当n=4时,Sn取得最小值 |
| D、当n=3时,Sn取得最大值 |
已知向量
,
的模均为2,且<
,
>=
,若向量
满足|
-(
+
)|=
,则|
|的取值范围为( )
| a |
| b |
| a |
| b |
| 2π |
| 3 |
| c |
| c |
| a |
| b |
| 2 |
| c |
A、[2-
| ||||
B、[0,2+
| ||||
C、[2-
| ||||
| D、[0,4] |