题目内容
下列函数在（-∞，0）上为减函数的是（ ）
| A、y=-x2 |
| B、y=x-1 |
| C、y=2x+1 |
| D、y=2x |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：根据二次函数、反比例函数、一次函数，以及指数函数的单调性即可找出正确选项．
解答：
解：二次函数y=-x2在（-∞，0）上为增函数，所以A错误；
反比例函数y=x-1在（-∞，0）上为减函数，所以B正确；
一次函数y=2x+1在（-∞，0）上为增函数，所以C错误；
指数函数y=2x在（-∞，0）上为增函数，所以D错误．
故选B．
反比例函数y=x-1在（-∞，0）上为减函数，所以B正确；
一次函数y=2x+1在（-∞，0）上为增函数，所以C错误；
指数函数y=2x在（-∞，0）上为增函数，所以D错误．
故选B．
点评：考查二次函数、反比例函数、一次函数、指数函数的单调性，注意二次函数的开口方向．
练习册系列答案
相关题目
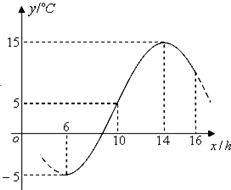如图，某地一天6-16时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b，其中A＞0，ω＞0，0＜φ＜π．已知平面向量
=（1，2），
=（x，1），如果向量
+2
与2
-
平行，那么
•（
-
）等于（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、-2 | ||
| B、-1 | ||
C、
| ||
D、
|