Question

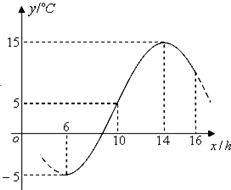如图，某地一天6-16时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b，其中A＞0，ω＞0，0＜φ＜π．
（1）求这一天6～16时的最大温差；
（2）根据图象确定这段曲线的函数解析式；
（3）估计16时的气温大概是多少°C？（结果精确到0.1°C，参考数据：

2

≈1.414，

3

≈1.732）．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正弦函数的图象,在实际问题中建立三角函数模型

专题：应用题,三角函数的图像与性质

分析：（1）由图可得：最大温差为15-（-5）=20（°C）；
（2）根据图象可求得：A，b的值，由（6，-5）在图象上，从而可求得φ，即可求得解析式．
（3）由函数的解析式从而可求得x=16时的函数值．

解答： （12分）
解：（1）最大温差为15-（-5）=20（°C）．
（2）∵依题意，A=10，b=5，T=2×（14-6）=16，ω=

π

8

，
由10sin（

π

8

×6+φ）+5=-5，又0＜φ＜π，
∴φ=

3π

4

，
∴y=10sin（

π

8

x+

3π

4

）+5，x∈[6，16]
（3）x=16时，y=10sin（

π

8

×16+

3π

4

）+5≈12.1（°C）

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，确定参数A，ω，ϕ，b的值即函数解析式是关键，属于中档题．