题目内容
在平面直角坐标系中,O是坐标原点,已知向量
=(2,a)(a∈R),则“a=-1”是“点M在第四象限”的( )
| OM |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:函数的性质及应用
分析:根据向量坐标与点的坐标之间的关系结合充分条件和必要条件的定义即可得到结论.
解答:
解:∵向量
=(2,a),∴M=(2,a),
若a=-1,则M=(2,-1)位于第四象限,
若M位于第四象限,则满足a<0,当a=-2时,满足条件,但a=-1不成立,
故“a=-1”是“点M在第四象限”的充分性不成立,
故选:A
| OM |
若a=-1,则M=(2,-1)位于第四象限,
若M位于第四象限,则满足a<0,当a=-2时,满足条件,但a=-1不成立,
故“a=-1”是“点M在第四象限”的充分性不成立,
故选:A
点评:本题主要考查充分条件和必要条件的判断,根据向量坐标与点的坐标之间的关系是解决本题的关键.

练习册系列答案
相关题目
一项“过关游戏”规则规定:在第n关要抛掷一颗骰子n次,如果这n次抛掷所出现的点数的和大于2n”,则算过关,则某人连过前三关的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=(
)x-x
,那么在下列区间中含有函数f(x)零点的是( )
| 1 |
| 2 |
| 1 |
| 3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(0,
|
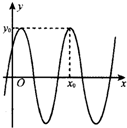 函数f(x)=3sin(2x+
函数f(x)=3sin(2x+