题目内容
一项“过关游戏”规则规定:在第n关要抛掷一颗骰子n次,如果这n次抛掷所出现的点数的和大于2n”,则算过关,则某人连过前三关的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:等可能事件的概率
专题:概率与统计
分析:分别求出第一、二、三关过关的概率,利用概率的乘法公式,可得结论.
解答:
解:(1)要求他第一关时掷1次的点数>2,第二关时掷2次的点数和>4,第三关时掷3次的点数和>8.
第一关过关的概率=
=
;
第二关过关的基本事件有62种,不能过关的基本事件为不等式x+y≤4的正整数解的个数,有
个 (亦可枚举计数:1+1,1+2,1+3,2+1,2+2,3+1)计6种,
过关的概率=1-
=
;
第三关的基本事件有63种,不能过关的基本事件为方程x+y+z≤8的正整数解的总数,可连写8个1,从8个空档中选3个空档的方法为
=56=56种,不能过关的概率=
=
,能过关的概率=1-
=
;
∴连过三关的概率=
×
×
=
.
故选A.
第一关过关的概率=
| 4 |
| 6 |
| 2 |
| 3 |
第二关过关的基本事件有62种,不能过关的基本事件为不等式x+y≤4的正整数解的个数,有
| C | 2 4 |
过关的概率=1-
| 6 |
| 62 |
| 5 |
| 6 |
第三关的基本事件有63种,不能过关的基本事件为方程x+y+z≤8的正整数解的总数,可连写8个1,从8个空档中选3个空档的方法为
| C | 3 8 |
| 56 |
| 63 |
| 7 |
| 27 |
| 7 |
| 27 |
| 20 |
| 27 |
∴连过三关的概率=
| 2 |
| 3 |
| 5 |
| 6 |
| 20 |
| 27 |
| 100 |
| 243 |
故选A.
点评:本题考查相互独立事件的概率乘法公式,考查学生分析解决问题的能力,确定基本事件的个数是关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
我班制定了数学学习方案:星期一和星期日分别解决4个数学问题,且从星期二开始,每天所解决问题的个数与前一天相比,要么“多一个”要么“持平”要么“少一个”.在一周中每天所解决问题个数的不同方案共有( )
| A、50种 | B、51种 |
| C、140种 | D、141种 |
已知正方体ABCD-A1B1C1D1,E,F是BD上的动点,是AD1上的动点,则( )
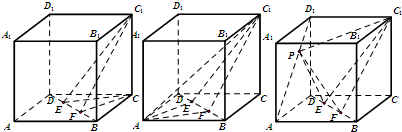

| A、VC-C1EF=VA-C1EF=VP-C1EF |
| B、VC-C1EF=VA-C1EF<VP-C1EF |
| C、VC-C1EF=VA-C1EF>VP-C1EF |
| D、VC-C1EF<VA-C1EF<VP-C1EF |
在平面直角坐标系中,O是坐标原点,已知向量
=(2,a)(a∈R),则“a=-1”是“点M在第四象限”的( )
| OM |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |