题目内容
已知点A（1，-2）若向量
与
=（2，3）同向，|
|=
，则点B的坐标为 ．
| AB |
| a |
| AB |
| 13 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量共线定理、模的计算公式即可得出．
解答：
解：设B（x，y），
=（x-1，y+2）．
∵向量
与
=（2，3）同向，
∴3（x-1）-2（y+2）=0，
∵|
|=
，
∴
=
．
化为（x-1）2+（y+2）2=13，
联立
，
解得
，
．
当
时，向量
与
=（2，3）反向，
∴B（3，1）．
故答案为：（3，1）．
| AB |
∵向量
| AB |
| a |
∴3（x-1）-2（y+2）=0，
∵|
| AB |
| 13 |
∴
| (x-1)2+(y+2)2 |
| 13 |
化为（x-1）2+（y+2）2=13，
联立
|
解得
|
|
当
|
| AB |
| a |
∴B（3，1）．
故答案为：（3，1）．
点评：本题考查了向量共线定理、模的计算公式，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=|x+2|+1，g（x）=ax．若关于x的方程f（x）=g（x）有两个不相等的实根，则实数a的取值范围是（ ）
A、（-1，-
| ||
B、（
| ||
C、（0，
| ||
| D、（-∞，-1） |
下列式子正确的是（ ）
A、
| ||||||||||||
B、
| ||||||||||||
C、λ（μa）=（λμ）
| ||||||||||||
D、
|
在平面直角坐标系中，O是坐标原点，已知向量
=（2，a）（a∈R），则“a=-1”是“点M在第四象限”的（ ）
| OM |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设a∈R，若函数y=ex+ax，x∈R，有大于-1的极值点，则（ ）
| A、a＜-1 | ||
| B、a＞-1 | ||
C、a＜-
| ||
D、a＞-
|
下列有关命题的说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、命题“若x=y，则sinx≠siny”的逆否命题为假命题 |
| D、命题“若x2+y2≠0，则x、y不全为零”的否命题为真命题 |
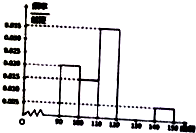某校高三数学竞赛初赛考试后，对考生的成绩进行统计（考生成绩均不低于90分，满分为150分），将成绩按如下方式分成六组，第一组[90，100）、第二组[100，110）…，第六组[140，150]，如图为其频率分布直方图的一部分，若第四、五、六组的人数依次成等差数列，且第六组有4人．