题目内容
函数由如表定义,若a0=5,an+1=f(an),n=0,1,2,…,则a2014=( )
| x | 2 | 5 | 3 | 1 | 4 |
| f(x) | 1 | 2 | 3 | 4 | 5 |
| A、1 | B、2 | C、3 | D、5 |
考点:数列递推式
专题:函数的性质及应用
分析:根据表格中的对应函数关系,得到an取值的规律性,即可得到结论.
解答:
解:由表格数据关系可得a0=5,
a1=f(a0)=f(5)=2,
a2=f(a1)=f(2)=1,
a3=f(a2)=f(1)=4,
a4=f(a3)=f(4)=5,
a5=f(a4)=f(5)=2,
…,
则an,的取值具备周期性,
周期数为4,
则a2014=a503×4+2=a2=1,
故选:A
a1=f(a0)=f(5)=2,
a2=f(a1)=f(2)=1,
a3=f(a2)=f(1)=4,
a4=f(a3)=f(4)=5,
a5=f(a4)=f(5)=2,
…,
则an,的取值具备周期性,
周期数为4,
则a2014=a503×4+2=a2=1,
故选:A
点评:本题主要考查函数值的计算,根据表格数据,得到an取值的规律性是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知平面直角坐标系xOy内直线l的参数方程为
(t为参数),以Ox为极轴建立极坐标系(取相同的长度单位),圆C的极坐标方程为ρ=2
sin(θ+
),则直线l与圆C的公共点的个数为 .
|
| 2 |
| π |
| 4 |
在△ABC中,设命题p:
=
=
,命题q:△ABC是等边三角形,那么命题p是命题q的( )
| a |
| sinC |
| b |
| sinA |
| c |
| sinB |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若关于x的两个方程a1-x=x,a1+x=-x的解分别为m,n(其中a>1的常数),则m+n的值( )
| A、大于0 |
| B、小于0 |
| C、等于0 |
| D、以上值都不对,与a的值有关 |
已知复数z=(a2-1)+(a-2)i(a∈R)是纯虚数,则a=( )
| A、1 | B、-1 | C、-1或1 | D、2 |
一个几何体按比例绘制的三视图如图所示(单位:m)
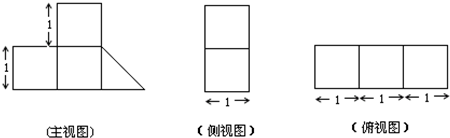
则该几何体的表面积为( )m3.

则该几何体的表面积为( )m3.
| A、14 | ||
| B、15 | ||
C、14+
| ||
D、15+
|