题目内容
一个几何体按比例绘制的三视图如图所示（单位：m）
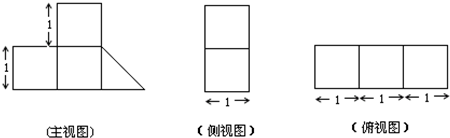
则该几何体的表面积为（ ）m3．
则该几何体的表面积为（ ）m3．
| A、14 | ||
| B、15 | ||
C、14+
| ||
D、15+
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：通过三视图判断几何体的形状，结合三视图的数据求解几何体的表面积即可．
解答：
解：由三视图可知组合体是由三个正方体与一个三棱柱（正方体的一半）组成的，正方体的棱长为1，
组合体的表面积是：左边正方体的5个面，上部正方体的5个面，中间正方体的3个面，三棱柱的上底面下底面，1个正方形和1个侧面，共计15个正方形与1个矩形，15+1×
=15+
．
故选：D．
组合体的表面积是：左边正方体的5个面，上部正方体的5个面，中间正方体的3个面，三棱柱的上底面下底面，1个正方形和1个侧面，共计15个正方形与1个矩形，15+1×
| 2 |
| 2 |
故选：D．
点评：本题考查组合体的表面积，三视图复原几何体是解题的关键，考查计算能力与空间想象能力．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
已知实数x，y满足
，若z=x2+y2，则z的最小值为（ ）
|
| A、1 | ||
B、
| ||
C、
| ||
| D、4 |
已知定义在R上的函数f（x）满足f（x）+2f（
）=3x，则f（2014）=（ ）
| x+2012 |
| x-1 |
| A、0 | B、2010 |
| C、-2010 | D、2014 |
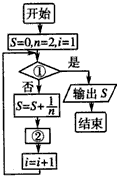如图给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 108 |
| A、i＞108，n=n+1 |
| B、i＞108，n=n+2 |
| C、i＞54，n=n+2 |
| D、i≤54，n=n+2 |
正项等比数列{an}中，若2a48a52=16，则a1a99等于（ ）
| A、-16 | B、8 | C、16 | D、4 |