题目内容
在△ABC中，设命题p：
=
=
，命题q：△ABC是等边三角形，那么命题p是命题q的（ ）
| a |
| sinC |
| b |
| sinA |
| c |
| sinB |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据正弦定理，利用充分条件和必要条件的定义进行判断即可得到结论．
解答：
解：由正弦定理可知
=
=
，若
=
=
=t，
则
=
=
=t，
即a=tc，b=ta，c=bt，
即abc=t3abc，即t=1，
则a=b=c，即△ABC是等边三角形，
若△ABC是等边三角形，则A=B=C=
，则
=
=
=1成立，
即命题p是命题q的充要条件，
故选：C
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| a |
| sinC |
| b |
| sinA |
| c |
| sinB |
则
| a |
| c |
| b |
| a |
| c |
| b |
即a=tc，b=ta，c=bt，
即abc=t3abc，即t=1，
则a=b=c，即△ABC是等边三角形，
若△ABC是等边三角形，则A=B=C=
| π |
| 3 |
| a |
| sinC |
| b |
| sinA |
| c |
| sinB |
即命题p是命题q的充要条件，
故选：C
点评：本题主要考查充分条件和必要条件的判断，利用正弦定理是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在正四面体ABCD中，E、F、G分别是BC、CD、DB的中点，下面四个结论中不正确的是（ ）
| A、BC∥平面AGF |
| B、EG⊥平面ABF |
| C、平面AEF⊥平面BCD |
| D、平面ABF⊥平面BCD |
对于定义域为D的函数y=f（x）和常数C，若对任意正实数ξ，存在x∈D，使得0＜|f（x）-c|＜ξ恒成立，则称函数y=f（x）为“敛C函数”．现给出如下函数：
①f（x）=x（x∈Z）； ②f（x）=（
）x+1（x∈Z）；③f（x）=log2x； ④f（x）=
．
其中为“敛1函数”的有（ ）
①f（x）=x（x∈Z）； ②f（x）=（
| 1 |
| 2 |
| x-1 |
| x |
其中为“敛1函数”的有（ ）
| A、①② | B、③④ |
| C、②③④ | D、①②③ |
定义区间[a，b]的长度为b-a．若[
，
]是函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜π）一个长度最大的单调递减区间，则（ ）
| π |
| 4 |
| π |
| 2 |
A、ω=8，φ=
| ||
B、ω=8，φ=-
| ||
C、ω=4，φ=
| ||
D、ω=4，φ=-
|
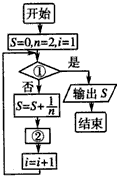如图给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 108 |
| A、i＞108，n=n+1 |
| B、i＞108，n=n+2 |
| C、i＞54，n=n+2 |
| D、i≤54，n=n+2 |