题目内容
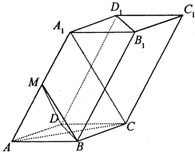 已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AA1=2
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AA1=2| 2 |
(Ⅰ)求证:A1C∥平面BMD;
(Ⅱ)求点C1到平面BDD1B1的距离.
考点:点、线、面间的距离计算,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)连结MO,由已知条件推导出MO∥A1C,由此能证明A1C∥平面BMD;
(Ⅱ)设C1H为C1到平面BDD1B1的距离,证明A1O⊥平面ABCD,利用等体积,结合点B到平面A1B1C1D1的距离等于点A1到平面ABCD的距离A1O=3,可得点C1到平面BDD1B1的距离.
(Ⅱ)设C1H为C1到平面BDD1B1的距离,证明A1O⊥平面ABCD,利用等体积,结合点B到平面A1B1C1D1的距离等于点A1到平面ABCD的距离A1O=3,可得点C1到平面BDD1B1的距离.
解答:
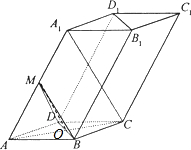 (Ⅰ)证明:AC∩BD=O,连结MO,
(Ⅰ)证明:AC∩BD=O,连结MO,
∵A1M=MA,AO=OC,
∴MO∥A1C,
∵MO?平面BMD,A1C不包含于平面BMD,
∴A1C∥平面BMD
(Ⅱ)解:设过C1作C1H⊥平面BDD1B1于H,则
∵BD⊥A1A,BD⊥AC,A1A∩AC=A,
∴BD⊥平面A1AC,
∴BD⊥A1O,
∵四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,∠BAD=60°,
∴AO=
AC=
,
∵AA1=2
,∠A1AC=60°,
∴A1O⊥AC,
∵AC∩BD=O,
∴A1O⊥平面ABCD
又∵平面ABCD∥平面A1B1C1D1,∴点B到平面A1B1C1D1的距离等于点A1到平面ABCD的距离A1O=3VB-B1C1D1=VC1-BB1D1?
•A1O•
×2×
=
•C1H•
×2×2
⇒C1H=
.
 (Ⅰ)证明:AC∩BD=O,连结MO,
(Ⅰ)证明:AC∩BD=O,连结MO,∵A1M=MA,AO=OC,
∴MO∥A1C,
∵MO?平面BMD,A1C不包含于平面BMD,
∴A1C∥平面BMD
(Ⅱ)解:设过C1作C1H⊥平面BDD1B1于H,则
∵BD⊥A1A,BD⊥AC,A1A∩AC=A,
∴BD⊥平面A1AC,
∴BD⊥A1O,
∵四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,∠BAD=60°,
∴AO=
| 1 |
| 2 |
| 3 |
∵AA1=2
| 3 |
∴A1O⊥AC,
∵AC∩BD=O,
∴A1O⊥平面ABCD
又∵平面ABCD∥平面A1B1C1D1,∴点B到平面A1B1C1D1的距离等于点A1到平面ABCD的距离A1O=3VB-B1C1D1=VC1-BB1D1?
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
点评:本题考查线面平行,考查点到平面距离的计算,考查学生分析解决问题的能力,掌握直线与平面平行的证明方法是关键.

练习册系列答案
相关题目
点M的直角坐标为(-
,-1)化为极坐标为( )
| 3 |
A、(2,
| ||
B、(2,
| ||
C、(2,
| ||
D、(2,
|
命题“?x>0,sinx=0”的否定为( )
| A、?x>0,sinx≠0 |
| B、?x≤0,sinx≠0 |
| C、?x≤0,sinx≠0 |
| D、?x>0,sinx≠0 |
设直线y=
x与圆C:(x-2)2+y2=4交于A,B两点,则弦长|AB|=( )
| 3 |
A、
| ||
B、2
| ||
| C、1 | ||
| D、2 |
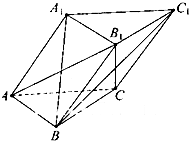 已知三棱柱ABC-A1B1C1中,底面边长和侧棱长均为a,侧面A1ACC1⊥底面ABC,A1B=
已知三棱柱ABC-A1B1C1中,底面边长和侧棱长均为a,侧面A1ACC1⊥底面ABC,A1B=