题目内容
设直线y=
x与圆C：（x-2）2+y2=4交于A，B两点，则弦长|AB|=（ ）
| 3 |
A、
| ||
B、2
| ||
| C、1 | ||
| D、2 |
考点：直线与圆相交的性质
专题：直线与圆
分析：由题意求得圆心和半径r，求得弦心距d的值，再由弦长|AB|=2
，计算求得结果．
| r2-d2 |
解答：
解：由题意可得，圆心C（2，0），半径r=2，
求得弦心距d=
=
，∴弦长|AB|=2
=2，
故选：D．
求得弦心距d=
|2
| ||
|
| 3 |
| r2-d2 |
故选：D．
点评：本题主要考查直线和圆的位置关系，点到直线的距离公式，弦长公式的应用，属于基础题．
练习册系列答案
相关题目
某市在一次降雨过程中，降雨量y（mm）与时间t（min）的函数关系可近似地表示为y=f（t）=
，则在时刻t=40min的降雨强度为（ ）
| 10t |
| A、20mm/min | ||
| B、400mm/min | ||
C、
| ||
D、
|
为得到函数y=sin（x+
）的图象，可将函数y=cosx的图象向右平移m（m＞0）个单位长度，则m的最小值是（ ）
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在区间[1，3]上任取一数，则这个数大于等于1.5的概率为（ ）
| A、0.25 | B、0.5 |
| C、0.6 | D、0.75 |
设Sn是等差数列{an}的前n项和，若
=
，则
（ ）
| S3 |
| S6 |
| 1 |
| 3 |
| S6 |
| S11 |
A、
| ||
B、
| ||
C、
| ||
D、
|
化简
-
+
=（ ）
| AC |
| DC |
| DA |
A、
| ||
B、
| ||
C、
| ||
D、
|
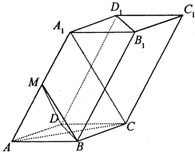已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形，AA1=2
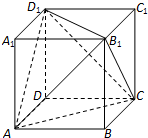如图，已知正方体ABCD-A1B1C1D1的棱长为1．
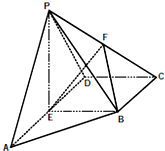如图，在四棱锥P-ABCD中，E为AD的中点，F为PC的中点，PE⊥平面ABCD，AD∥BC，AD⊥CD，且BC=CD=