题目内容
已知数列{an}中,a1=4.
(1)若an=an+1+3,求a10;
(2)若数列{
}为等差数列,且a6=
,求数列{an}的通项公式.
(1)若an=an+1+3,求a10;
(2)若数列{
| 1 |
| an |
| 1 |
| 4 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:(1)由an=an+1+3,知{an}为等差数列,由此能求出求a10.
(2)若数列{
}为等差数列,由
=
,
=4,得d=
=
,由此能求出an=
.
(2)若数列{
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| 4 |
| 1 |
| a6 |
| ||||
| 6-1 |
| 3 |
| 4 |
| 4 |
| 3n-2 |
解答:
(本题满分8分)
解:(1)由an=an+1+3,知{an}为等差数列,公差为-3,
∴a10=a1+9d=4+9×(-3)=-23.(4分)
(2)若数列{
}为等差数列,由
=
,
=4,
得d=
=
,
∴
=
+(n-1)d=
+
(n-1)=
,
∴an=
.(8分)
解:(1)由an=an+1+3,知{an}为等差数列,公差为-3,
∴a10=a1+9d=4+9×(-3)=-23.(4分)
(2)若数列{
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| 4 |
| 1 |
| a6 |
得d=
| ||||
| 6-1 |
| 3 |
| 4 |
∴
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3n-2 |
| 4 |
∴an=
| 4 |
| 3n-2 |
点评:本题考查数列的第10项和求法,考查数列的通项公式的求法,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为得到函数y=sin(x+
)的图象,可将函数y=cosx的图象向右平移m(m>0)个单位长度,则m的最小值是( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
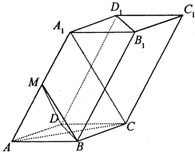 已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AA1=2
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AA1=2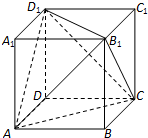 如图,已知正方体ABCD-A1B1C1D1的棱长为1.
如图,已知正方体ABCD-A1B1C1D1的棱长为1.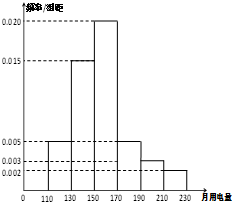 2013年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
2013年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.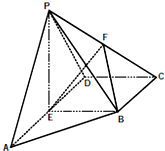 如图,在四棱锥P-ABCD中,E为AD的中点,F为PC的中点,PE⊥平面ABCD,AD∥BC,AD⊥CD,且BC=CD=
如图,在四棱锥P-ABCD中,E为AD的中点,F为PC的中点,PE⊥平面ABCD,AD∥BC,AD⊥CD,且BC=CD=