题目内容
设函数f(x)=2x3+3ax2+3bx+8在x=1及x=2时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的x∈[0,3],求函数f(x)的最值.
(Ⅲ)若对x∈[0,3],不等式f(x)<m恒成立,求m的取值范围.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的x∈[0,3],求函数f(x)的最值.
(Ⅲ)若对x∈[0,3],不等式f(x)<m恒成立,求m的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值,导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(I)利用导数的运算法则可得:f′(x)=6x2+6ax+3b,由于函数f(x)在x=1及x=2时取得极值.可知:1,2是方程f′(x)=0的两个实数根,利用根与系数的关系可得,再进行验证即可;
(II)列出表格,利用导数与函数单调性的关系,即可得出极值与最值;
(III)对x∈[0,3],不等式f(x)<m恒成立?m>[f(x)]max,由(II)即可得出.
(II)列出表格,利用导数与函数单调性的关系,即可得出极值与最值;
(III)对x∈[0,3],不等式f(x)<m恒成立?m>[f(x)]max,由(II)即可得出.
解答:
解:(I)f′(x)=6x2+6ax+3b,
∵函数f(x)在x=1及x=2时取得极值.
∴1,2是方程f′(x)=0的两个实数根,
∴1+2=-a,1×2=
,解得a=-3,b=4.
经验证a=-3,b=4满足条件.
∴a=-3,b=4.
(II)由(I)可得:f(x)=2x3-9x2+12x+8.
f′(x)=6x2-18x+12=6(x-1)(x-2).
列出表格:
由表格可知:当x=1时,函数f(x)取得极大值,f(1)=13,又f(3)=17,∴函数f(x)的最大值为17;当x=2时,函数f(x)取得极小值,f(2)=12,又f(0)=8,∴函数f(x)的最小值为8.
综上可得:当x=3时,函数f(x)取得最大值17;当x=0时,函数f(x)取得最小值8.
(III)对x∈[0,3],不等式f(x)<m恒成立?m>[f(x)]max,由(II)可得:函数f(x)的最大值为17,∴m>17.
∴m的取值范围是(17,+∞).
∵函数f(x)在x=1及x=2时取得极值.
∴1,2是方程f′(x)=0的两个实数根,
∴1+2=-a,1×2=
| b |
| 2 |
经验证a=-3,b=4满足条件.
∴a=-3,b=4.
(II)由(I)可得:f(x)=2x3-9x2+12x+8.
f′(x)=6x2-18x+12=6(x-1)(x-2).
列出表格:
| x | [0,1) | 1 | (1,2) | 2 | (2,3] |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
综上可得:当x=3时,函数f(x)取得最大值17;当x=0时,函数f(x)取得最小值8.
(III)对x∈[0,3],不等式f(x)<m恒成立?m>[f(x)]max,由(II)可得:函数f(x)的最大值为17,∴m>17.
∴m的取值范围是(17,+∞).
点评:本题考查了利用导数研究函数的单调性极值与最值,考查了恒成立问题的等价转化方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
椭圆
+
=1上一点满足∠F1PF2=60°(F1,F2为焦点),则△F1PF2的面积为( )
| y2 |
| 25 |
| x2 |
| 9 |
| A、3 | ||||
B、3
| ||||
C、
| ||||
D、6
|
设Sn是等差数列{an}的前n项和,若
=
,则
( )
| S3 |
| S6 |
| 1 |
| 3 |
| S6 |
| S11 |
A、
| ||
B、
| ||
C、
| ||
D、
|
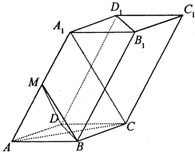 已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AA1=2
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AA1=2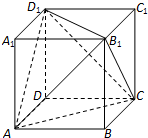 如图,已知正方体ABCD-A1B1C1D1的棱长为1.
如图,已知正方体ABCD-A1B1C1D1的棱长为1.