题目内容
已知向量
=（
，1），
=（-2
，k），求
（1）k为何值时，
∥
？
（2）k为何值时，
⊥
？
| a |
| 3 |
| b |
| 3 |
（1）k为何值时，
| a |
| b |
（2）k为何值时，
| a |
| b |
考点：数量积判断两个平面向量的垂直关系,平行向量与共线向量
专题：平面向量及应用
分析：（1）由
∥
?x1y2-x2y1=0，求出k的值；
（2）由
⊥
?x1x2+y1y2=0，求出的值．
| a |
| b |
（2）由
| a |
| b |
解答：
解：（1）∵向量
=（
，1），
=（-2
，k），
∴
k-1×(-2
)=0，
解得k=-2；
∴当k=-2时，
∥
；
（2）∵向量
=（
，1），
=（-2
，k），
∴
(-2
)+1×k=0，
解得k=6；
∴当k=6时，
⊥
．
| a |
| 3 |
| b |
| 3 |
∴
| 3 |
| 3 |
解得k=-2；
∴当k=-2时，
| a |
| b |
（2）∵向量
| a |
| 3 |
| b |
| 3 |
∴
| 3 |
| 3 |
解得k=6；
∴当k=6时，
| a |
| b |
点评：本题考查了利用平面向量的数量积判定向量平行与垂直的问题，解题时应利用坐标运算表示向量的数量积，是基础题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
不等式x2•（x-1）＜0的解集是（ ）
| A、{x|x＞1} |
| B、{x|x＜1} |
| C、{x|0＜x＜1} |
| D、{x|x＜1，且x≠0} |
在区间[1，3]上任取一数，则这个数大于等于1.5的概率为（ ）
| A、0.25 | B、0.5 |
| C、0.6 | D、0.75 |
化简
-
+
=（ ）
| AC |
| DC |
| DA |
A、
| ||
B、
| ||
C、
| ||
D、
|
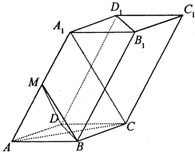已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形，AA1=2
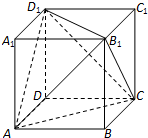如图，已知正方体ABCD-A1B1C1D1的棱长为1．
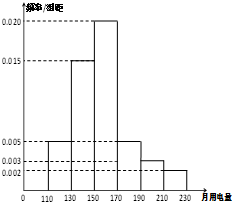2013年第三季度，国家电网决定对城镇居民民用电计费标准做出调整，并根据用电情况将居民分为三类：第一类的用电区间在（0，170]，第二类在（170，260]，第三类在（260，+∞）（单位：千瓦时）．某小区共有1000户居民，现对他们的用电情况进行调查，得到频率分布直方图如图所示．