题目内容
命题“?x＞0，sinx=0”的否定为（ ）
| A、?x＞0，sinx≠0 |
| B、?x≤0，sinx≠0 |
| C、?x≤0，sinx≠0 |
| D、?x＞0，sinx≠0 |
考点：命题的否定
专题：简易逻辑
分析：利用特称命题的否定是全称命题写出结果即可．
解答：
解：特称命题的否定是全称命题，
命题“?x＞0，sinx=0”的否定为：?x＞0，sinx≠0．
故选：D．
命题“?x＞0，sinx=0”的否定为：?x＞0，sinx≠0．
故选：D．
点评：本题考查命题的否定，特称命题与全称命题的否定关系．
练习册系列答案
相关题目
下列函数中同时具有①最小正周期是π；②图象关于点（
，0）对称这两个性质的是（ ）
| π |
| 6 |
A、y=cos（2x+
| ||||
B、y=sin（2x+
| ||||
C、y=sin（
| ||||
D、y=tan（x+
|
椭圆
+
=1上一点满足∠F1PF2=60°（F1，F2为焦点），则△F1PF2的面积为（ ）
| y2 |
| 25 |
| x2 |
| 9 |
| A、3 | ||||
B、3
| ||||
C、
| ||||
D、6
|
为得到函数y=sin（x+
）的图象，可将函数y=cosx的图象向右平移m（m＞0）个单位长度，则m的最小值是（ ）
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中，a，b，c分别是角A、B、C的对边，若a=1，且2cosC+c=2b，则△ABC的周长的取值范围是（ ）
| A、（1，3] |
| B、[2，4] |
| C、（2，3] |
| D、[3，5] |
在区间[1，3]上任取一数，则这个数大于等于1.5的概率为（ ）
| A、0.25 | B、0.5 |
| C、0.6 | D、0.75 |
设Sn是等差数列{an}的前n项和，若
=
，则
（ ）
| S3 |
| S6 |
| 1 |
| 3 |
| S6 |
| S11 |
A、
| ||
B、
| ||
C、
| ||
D、
|
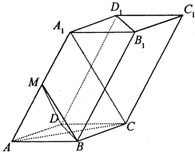已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形，AA1=2