题目内容
在△ABC中，角A，B，C所对的边分别为a，b，c，若（a2+c2-b2）tanB=
ac，则sinB的值为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：余弦定理
专题：计算题,三角函数的求值,解三角形
分析：已知等式变形后，利用余弦定理化简，再利用同角三角函数间的基本关系化简求出sinB的值．
解答：
解：由于（a2+c2-b2）tanB=
ac，
则有：
•tanB=cosB•tanB=cosB•
=sinB=
，
故选B．
| 3 |
则有：
| a2+c2-b2 |
| 2ac |
| sinB |
| cosB |
=sinB=
| ||
| 2 |
故选B．
点评：此题考查了余弦定理，以及同角三角函数间的基本关系，熟练掌握余弦定理是解本题的关键．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知函数f（x）=|x2-4x+3|，若方程[f（x）]2+bf（x）+c=0恰有七个不相同的实根，则实数b的取值范围是（ ）
| A、（-2，0） |
| B、（-2，-1） |
| C、（0，1） |
| D、（0，2） |
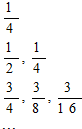如图给出了一个“直角三角形数阵”：满足每一列成等差数列，从第三行起，每一行的数成等比数列，且每一行的公比相等，记第i行第j列的数为aij（i≥j，i，j∈N*），则a88=已知a，b，c分别为△ABC角A、B、C所对的边，若满足a=
，b=
，A=45°，则角B的大小为（ ）
| 2 |
| 3 |
| A、90° | B、60° |
| C、60°或120° | D、120° |