题目内容
已知函数f(x)=|x2-4x+3|,若方程[f(x)]2+bf(x)+c=0恰有七个不相同的实根,则实数b的取值范围是( )
| A、(-2,0) |
| B、(-2,-1) |
| C、(0,1) |
| D、(0,2) |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:画出f(x)的图象,根据方程[f(x)]2+bf(x)+c=0恰有七个不相同的实根,可判断方程[f(x)]2+bf(x)+c=0恰有七个不相同的实根,再运用根的存在性定理可判断答案.
解答:
解:
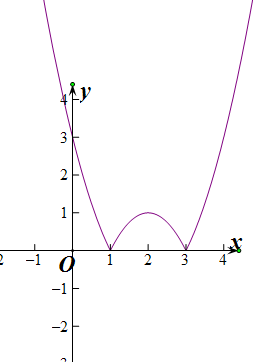
f(1)=f(3)=0,f(2)=1,
f(x)≥0,
∵若方程[f(x)]2+bf(x)+c=0恰有七个不相同的实根,
∴t2+bt+c=0,其中一个根为1,另一个根在(0,1)内,
∴g(t)=t2+bt+c,
g(1)=1+b+c=0,g(-
)<0,0<-
<1,g(0)=c>0方程[f(x)]2+bf(x)+c=0恰有七个不相同的实根
∴c=-1-b>0,b≠-2,-2<b<0,
即b的范围为:(-2,-1)
故选:B
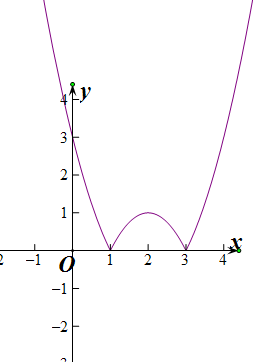
f(1)=f(3)=0,f(2)=1,
f(x)≥0,
∵若方程[f(x)]2+bf(x)+c=0恰有七个不相同的实根,
∴t2+bt+c=0,其中一个根为1,另一个根在(0,1)内,
∴g(t)=t2+bt+c,
g(1)=1+b+c=0,g(-
| b |
| 2 |
| b |
| 2 |
∴c=-1-b>0,b≠-2,-2<b<0,
即b的范围为:(-2,-1)
故选:B
点评:本题考查了函数的性质,图形,方程的根的分布问题,属于难题.

练习册系列答案
相关题目
已知函数f(x)=
x2+lnx,?x0∈[1,e],使不等式f(x)≤m,则实数m的取值范围( )
| 1 |
| 2 |
A、m≥1+
| ||
B、m≥
| ||
| C、m≥1 | ||
| D、m≥1+e |
在△ABC中,角A,B,C所对的边分别为a,b,c,若(a2+c2-b2)tanB=
ac,则sinB的值为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,某人在高出海面600米的山上P处,测得海面上的航标在A正东,俯角为30°,航标B在南偏东60°,俯角为45°,则这两个航标间的距离为
如图,某人在高出海面600米的山上P处,测得海面上的航标在A正东,俯角为30°,航标B在南偏东60°,俯角为45°,则这两个航标间的距离为