题目内容
数列{an}满足a1=2,an+1=
an,n∈N*,则an= .
| 2(n+2) |
| n+1 |
考点:数列递推式
专题:等差数列与等比数列
分析:由于所给的递推公式条件是后项与前一项的比值,故可由此推导从第二项起每一项与它前一项的比值直至第n项与第n-1项,然后采用叠乘法即可求出an.
解答:
解:由已知an+1=
an,得
=2×
,
=2×
…
=2×
,
=2×
,a1=2,
所以由an=
•
…
•
=2×
×2×
…×2×
×2×
=(n+1)2n-1
故答案为:(n+1)2n-1.
| 2(n+2) |
| n+1 |
| an+1 |
| an |
| n+2 |
| n+1 |
| an |
| an-1 |
| n+1 |
| n |
| a3 |
| a2 |
| 4 |
| 3 |
| a2 |
| a1 |
| 3 |
| 2 |
所以由an=
| an |
| an-1 |
| an-1 |
| an-2 |
| a3 |
| a2 |
| a2 |
| a1 |
| n+1 |
| n |
| n |
| n-1 |
| 4 |
| 3 |
| 3 |
| 2 |
故答案为:(n+1)2n-1.
点评:本题主要考查数列的求通项公式问题,所涉及的方法为叠乘法,属于中档题.

练习册系列答案
相关题目
在△ABC中,角A,B,C所对的边分别为a,b,c,若(a2+c2-b2)tanB=
ac,则sinB的值为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,某人在高出海面600米的山上P处,测得海面上的航标在A正东,俯角为30°,航标B在南偏东60°,俯角为45°,则这两个航标间的距离为
如图,某人在高出海面600米的山上P处,测得海面上的航标在A正东,俯角为30°,航标B在南偏东60°,俯角为45°,则这两个航标间的距离为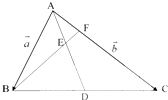 在△ABC中,D是BC中点,线段AD上的点E满足
在△ABC中,D是BC中点,线段AD上的点E满足