题目内容
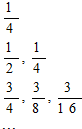 如图给出了一个“直角三角形数阵”:满足每一列成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N*),则a88=
如图给出了一个“直角三角形数阵”:满足每一列成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N*),则a88=考点:归纳推理
专题:计算题,推理和证明
分析:察这个“直角三角形数阵”,能够发现ai1=a11+(i-1)×
=
,再由从第三行起,每一行的数成等比数列,可求出aij(i≥j),即可得出结论.
| 1 |
| 4 |
| i |
| 4 |
解答:
解:ai1=a11+(i-1)×
=
,
aij=ai1×(
)j-1=
×(
)j-1=i×(
)j+1.
∴a88=8×(
)9=
故答案为:
.
| 1 |
| 4 |
| i |
| 4 |
aij=ai1×(
| 1 |
| 2 |
| i |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a88=8×(
| 1 |
| 2 |
| 1 |
| 64 |
故答案为:
| 1 |
| 64 |
点评:本题考查数列的性质和应用,解题时要仔细观察,耐心寻找数量间的相互关系,总结规律,认真解题.

练习册系列答案
相关题目
设函数f(x)=
+a是奇函数(a为常数),则f(x)<0的解集为( )
| 1 |
| 2x+1 |
| A、(0,+∞) | ||
| B、(1,+∞) | ||
| C、(-1,0)∪(0,1) | ||
D、(
|
在△ABC中,角A,B,C所对的边分别为a,b,c,若(a2+c2-b2)tanB=
ac,则sinB的值为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设{an}是等差数列,{bn}是等比数列,Sn、Tn分别是数列{an}、{bn}的前n项和.若a3=b3,a4=b4,且
=7,则
的值为( )
| S5-S3 |
| T4-T2 |
| a5 |
| b3+b6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
| 1-tan15° |
| 1+tan15° |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
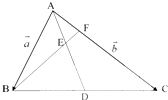 在△ABC中,D是BC中点,线段AD上的点E满足
在△ABC中,D是BC中点,线段AD上的点E满足