题目内容
[x]表示不超过x的最大整数,数列{an},{bn}分别满足an=[10nx]-10[10n-1x],bn=[
]-[
],其中k∈N,k<10,Sn为数列{bn}的前n项和,当x=
,k=7时,则S100=( )
| an+1 |
| k+1 |
| an+1 |
| k+1.01 |
| 1 |
| 7 |
| A、16 | B、32 | C、33 | D、34 |
考点:数列的求和
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:运用列举法求出前7项,可判断是周期为6的数列,再利用周期性求解S100即可解决.
解答:
解:∵[x]表示不超过x的最大整数,数列{an},{bn}分别满足:
an=[10nx]-10[10n-1x],bn=[
]-[
],
其中k∈N,k<10,Sn为数列{bn}的前n项和,当x=
,k=7,
∴a1=1,b1=;,a2=4,b2=0;a3=2,b3=0;a4=8,b4=0;a5=5,b5=0;a6=7,b6=1;a7=1,b7=0,
周期性为6,
100÷6=16余数为4,
S100=16,
故选:A
an=[10nx]-10[10n-1x],bn=[
| an+1 |
| k+1 |
| an+1 |
| k+1.01 |
其中k∈N,k<10,Sn为数列{bn}的前n项和,当x=
| 1 |
| 7 |
∴a1=1,b1=;,a2=4,b2=0;a3=2,b3=0;a4=8,b4=0;a5=5,b5=0;a6=7,b6=1;a7=1,b7=0,
周期性为6,
100÷6=16余数为4,
S100=16,
故选:A
点评:本题考查了列举法求解数列的和的问题,主要考察能够大胆列举,不受题意的表面现象影响.

练习册系列答案
相关题目
以双曲线
-
=1的右顶点为焦点的抛物线的标准方程是( )
| x2 |
| 4 |
| y2 |
| 9 |
| A、y2=4x |
| B、y2=16x |
| C、y2=8x |
| D、y2=-8x |
在等比数列{an}中,a5•a11=3,a3+a13=4,则
=( )
| a25 |
| a5 |
| A、3 | ||
| B、9 | ||
C、3或
| ||
D、9或
|
若x∈R,则x=2”是“(x-2)(x-1)=0”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
设△ABC的内角A,B,C所对的边分别为a,b,c.若(a+b-c)(a+b+c)=ab,则角C=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
| B、命题“?x≥0,x2+x-1<0”的否定是“?x0<0,x02+x0-1≥0” |
| C、命题“若x=y,则sin x=sin y”的逆否命题为假命题 |
| D、若“p∨q”为真命题,则p,q中至少有一个为真命题 |
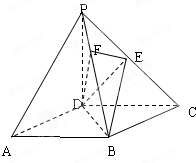 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB于点F.