题目内容
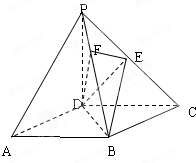 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB于点F.(1)求证:面PBC⊥面EFD;
(2)求二面角C-PB-D的正切值大小.
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)根据已知条件便知,DE⊥BC,DE⊥PC,所以DE⊥平面PBC,所以PB⊥DE,又PB⊥EF,所以PD⊥平面DEF,所以面PBC⊥面EFD;
(2)通过(1)知∠DFE是二面角C-PB-D的平面角,并且△DEF是直角三角形,设PD=1,容易求出DE=
,根据△PEF∽△PBC,可求出EF,继而求出DF,则二面角C-PB-D的正切值便是:
,把求得的DE,DF带入即可.
(2)通过(1)知∠DFE是二面角C-PB-D的平面角,并且△DEF是直角三角形,设PD=1,容易求出DE=
| ||
| 2 |
| DE |
| DF |
解答:
解:(1)证明:∵PD⊥底面ABCD,BC?底面ABCD;
∴PD⊥BC,即BC⊥PD,又BC⊥CD,PD∩CD=D;
∴BC⊥平面PCD,DE?平面PCD,∴BC⊥DE,即DE⊥BC;
∵PD=DC,E是PC的中点;
∴DE⊥PC,PC∩BC=C;
∴DE⊥平面PBC,PB?平面PBC;
∴DE⊥PB,即PB⊥DE,又PB⊥EF,DE∩EF=E;
∴PB⊥平面EFD,PB?平面PBC;
∴平面PBC⊥平面EFD;
(2)PB⊥平面EFD,∴PB⊥EF,PB⊥DF;
∴∠DFE是二面角C-PB-D的平面角;
由(1)知DE⊥平面PBC,EF?平面PBC;
∴DE⊥EF,即△DEF为Rt△;
设PD=1,则DE=
;
由(1)知△PBC为Rt△,∴△PEF∽△PBC,∴
=
,∴EF=
;
在Rt△PDB中,PB=
=
,∴EF=
;
∴DF=
=
=
;
∴tan∠DFE=
=
=
.
∴PD⊥BC,即BC⊥PD,又BC⊥CD,PD∩CD=D;
∴BC⊥平面PCD,DE?平面PCD,∴BC⊥DE,即DE⊥BC;
∵PD=DC,E是PC的中点;
∴DE⊥PC,PC∩BC=C;
∴DE⊥平面PBC,PB?平面PBC;
∴DE⊥PB,即PB⊥DE,又PB⊥EF,DE∩EF=E;
∴PB⊥平面EFD,PB?平面PBC;
∴平面PBC⊥平面EFD;
(2)PB⊥平面EFD,∴PB⊥EF,PB⊥DF;
∴∠DFE是二面角C-PB-D的平面角;
由(1)知DE⊥平面PBC,EF?平面PBC;
∴DE⊥EF,即△DEF为Rt△;
设PD=1,则DE=
| ||
| 2 |
由(1)知△PBC为Rt△,∴△PEF∽△PBC,∴
| EF |
| BC |
| PE |
| PB |
| 1 |
| 2PB |
在Rt△PDB中,PB=
| 1+2 |
| 3 |
| ||
| 6 |
∴DF=
| DE2+EF2 |
|
| ||
| 6 |
∴tan∠DFE=
| DE |
| DF |
| ||||
|
| ||
| 7 |
点评:考查线面垂直的性质,线面垂直的判定定理,面面垂直的判定定理,二面角的概念,二面角的平面角,以及三角形相似.

练习册系列答案
相关题目
[x]表示不超过x的最大整数,数列{an},{bn}分别满足an=[10nx]-10[10n-1x],bn=[
]-[
],其中k∈N,k<10,Sn为数列{bn}的前n项和,当x=
,k=7时,则S100=( )
| an+1 |
| k+1 |
| an+1 |
| k+1.01 |
| 1 |
| 7 |
| A、16 | B、32 | C、33 | D、34 |
已知不等式ax2+bx-2>0的解集是{x|-2<x<-
},则a-b的值为( )
| 1 |
| 4 |
| A、2 | B、3 | C、4 | D、5 |
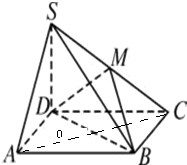 如图,底面ABCD是正方形,SD=AD,SD⊥底面ABCD,M为SC中点.求直线DM与SB所成的角的余弦值.
如图,底面ABCD是正方形,SD=AD,SD⊥底面ABCD,M为SC中点.求直线DM与SB所成的角的余弦值.