题目内容
设△ABC的内角A，B，C所对的边分别为a，b，c．若（a+b-c）（a+b+c）=ab，则角C=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：余弦定理
专题：解三角形
分析：已知等式左边利用平方差公式及完全平方公式化简，整理后利用余弦定理求出cosC的值，即可确定出C的度数．
解答：
解：∵（a+b-c）（a+b+c）=（a+b）2-c2=a2+b2-c2+2ab=ab，即a2+b2-c2=-ab，
∴cosC=
=-
，
则C=
．
故选：B．
∴cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
则C=
| 2π |
| 3 |
故选：B．
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
[x]表示不超过x的最大整数，数列{an}，{bn}分别满足an=[10nx]-10[10n-1x]，bn=[
]-[
]，其中k∈N，k＜10，Sn为数列{bn}的前n项和，当x=
，k=7时，则S100=（ ）
| an+1 |
| k+1 |
| an+1 |
| k+1.01 |
| 1 |
| 7 |
| A、16 | B、32 | C、33 | D、34 |
命题：
（1）?x∈R，2x-1＞0
（2）?x∈N*，（x-1）2＞0
（3）?x∈R，lgx＜1
（4）若p：
＞0，则?p：
≤0，
（5）?x∈R，sinx≥1
其中真命题个数是（ ）
（1）?x∈R，2x-1＞0
（2）?x∈N*，（x-1）2＞0
（3）?x∈R，lgx＜1
（4）若p：
| 1 |
| x-1 |
| 1 |
| x-1 |
（5）?x∈R，sinx≥1
其中真命题个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
已知不等式ax2+bx-2＞0的解集是{x|-2＜x＜-
}，则a-b的值为（ ）
| 1 |
| 4 |
| A、2 | B、3 | C、4 | D、5 |
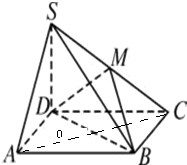如图，底面ABCD是正方形，SD=AD，SD⊥底面ABCD，M为SC中点．求直线DM与SB所成的角的余弦值．