题目内容
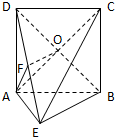
 在如图所示的几何体中,四边形ABCD为正方形,△ABE为直角三角形,∠BAE=90°,且AD⊥AE.
在如图所示的几何体中,四边形ABCD为正方形,△ABE为直角三角形,∠BAE=90°,且AD⊥AE.(Ⅰ)证明:平面AEC⊥平面BED;
(Ⅱ)若AB=2AE,求异面直线BE与AC所成角的余弦值.
考点:异面直线及其所成的角,平面与平面垂直的判定
专题:空间角
分析:(Ⅰ)由已知条件推导出AE⊥DB,DB⊥AC,由此能证明DB⊥平面AEC,从而得到平面AEC⊥平面BED.
(Ⅱ)作DE的中点F,连接OF,AF,由已知条件推导出∠FOA或其补角是异面直线BE与AC所成的角.由此能求出异面直线BE与AC所成的角的余弦值.
(Ⅱ)作DE的中点F,连接OF,AF,由已知条件推导出∠FOA或其补角是异面直线BE与AC所成的角.由此能求出异面直线BE与AC所成的角的余弦值.
解答:
 (Ⅰ)证明:由已知有AE⊥AB,又AE⊥AD,
(Ⅰ)证明:由已知有AE⊥AB,又AE⊥AD,
所以AE⊥平面ABCD,所以AE⊥DB,…(3分)
又ABCD为正方形,所以DB⊥AC,…(4分)
所以DB⊥平面AEC,BD?面BED
故有平面AEC⊥平面BED.…(6分)
(Ⅱ)解:作DE的中点F,连接OF,AF,
∵O是DB的中点,
∴OF∥BE,∴∠FOA或其补角是异面直线BE与AC所成的角.…(8分)
设正方形ABCD的边长为2a,
则AO=
a,…(9分)
∵∠BAE=90°,AB=2AE,
∴AE=a,EB=
a,∴OF=
a…(10分)
又AD⊥AE,∴AF=
ED=
a,∴cos∠FOA=
=
∴异面直线BE与AC所成的角的余弦值为
…(12分)
 (Ⅰ)证明:由已知有AE⊥AB,又AE⊥AD,
(Ⅰ)证明:由已知有AE⊥AB,又AE⊥AD,所以AE⊥平面ABCD,所以AE⊥DB,…(3分)
又ABCD为正方形,所以DB⊥AC,…(4分)
所以DB⊥平面AEC,BD?面BED
故有平面AEC⊥平面BED.…(6分)
(Ⅱ)解:作DE的中点F,连接OF,AF,
∵O是DB的中点,
∴OF∥BE,∴∠FOA或其补角是异面直线BE与AC所成的角.…(8分)
设正方形ABCD的边长为2a,
则AO=
| 2 |
∵∠BAE=90°,AB=2AE,
∴AE=a,EB=
| 5 |
| ||
| 2 |
又AD⊥AE,∴AF=
| 1 |
| 2 |
| ||
| 2 |
| OF2+OA2-AF2 |
| 2OF•OA |
| ||
| 5 |
∴异面直线BE与AC所成的角的余弦值为
| ||
| 5 |
点评:本题考查平面与平面垂直的证明,考查异面直线所成角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
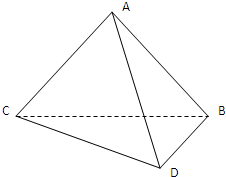 如图,平面ABC⊥平面DBC,已知AB=AC,BC=6,∠BAC=∠DBC=90°,∠BDC=60°
如图,平面ABC⊥平面DBC,已知AB=AC,BC=6,∠BAC=∠DBC=90°,∠BDC=60°  如图,一艘轮船在某海岛附近的海上匀速直线航行,海岛上一观察哨A在上午11时测得轮船在海岛北偏东60°的B处,12时20分测得轮船在海岛北偏西60°的C处,12时40分轮船到达位于海岛正西方且距离海岛5海里的D港口.
如图,一艘轮船在某海岛附近的海上匀速直线航行,海岛上一观察哨A在上午11时测得轮船在海岛北偏东60°的B处,12时20分测得轮船在海岛北偏西60°的C处,12时40分轮船到达位于海岛正西方且距离海岛5海里的D港口.