题目内容
已知:向量
=(1,2),
=(-3,2),向量
=k
+
,
=
-3
.
(1)当k为何值时,向量
∥
?
(2)若向量
与
的夹角为钝角,求实数k的取值范围的集合.
| e1 |
| e2 |
| x |
| e1 |
| e2 |
| y |
| e1 |
| e2 |
(1)当k为何值时,向量
| x |
| y |
(2)若向量
| x |
| y |
考点:数量积表示两个向量的夹角,平行向量与共线向量
专题:平面向量及应用
分析:(1)利用向量共线定理即可得出.
(2)若向量
与
的夹角为钝角,则
•
)<0,且向量
与
不能反向共线,解出即可.
(2)若向量
| x |
| y |
| x |
| y |
| x |
| y |
解答:
解:(1)∵向量
=(1,2),
=(-3,2),
∴向量
=k
+
=k(1,2)+(-3,2)=(k-3,2k+2)
=
-3
=(1,2)-3(-3,2)=(10,-4).
∵向量
∥
,∴-4(k-3)-10(2k+2)=0,解得k=-
.
∴当k=-
时,向量
∥
.
(2)若向量
与
的夹角为钝角,
则
•
=10(k-3)-4(2k+2)<0,且向量
与
不能反向共线,
解得x<19且x≠-
.
∴实数k的取值范围的集合为{x|x<19且x≠-
}.
| e1 |
| e2 |
∴向量
| x |
| e1 |
| e2 |
| y |
| e1 |
| e2 |
∵向量
| x |
| y |
| 1 |
| 3 |
∴当k=-
| 1 |
| 3 |
| x |
| y |
(2)若向量
| x |
| y |
则
| x |
| y |
| x |
| y |
解得x<19且x≠-
| 1 |
| 3 |
∴实数k的取值范围的集合为{x|x<19且x≠-
| 1 |
| 3 |
点评:本题考查了向量共线定理与向量夹角,属于基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
函数y=2x3-12x在区间[-1,3]上的最大值和最小值分别为( )
A、18,-8
| ||||
| B、54,-12 | ||||
C、8
| ||||
D、10,-8
|
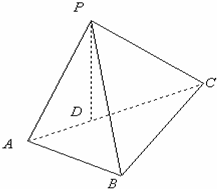 如图,三棱锥P-ABC,D为AC的中点,
如图,三棱锥P-ABC,D为AC的中点,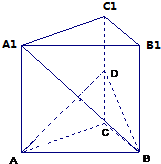 如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AC=BC=2,∠ACB=90°,侧棱AA1=2,D是CC1的中点.
如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AC=BC=2,∠ACB=90°,侧棱AA1=2,D是CC1的中点. 在如图所示的几何体中,四边形ABCD为正方形,△ABE为直角三角形,∠BAE=90°,且AD⊥AE.
在如图所示的几何体中,四边形ABCD为正方形,△ABE为直角三角形,∠BAE=90°,且AD⊥AE.