题目内容
已知
=（1，-1），
=（λ，1），
（1）当
⊥
时，求λ的值．
（2）若
与
的夹角α为钝角，求λ的取值范围．
| a |
| b |
（1）当
| a |
| b |
（2）若
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）由两向量垂直，得到
•
=0，由此方程即可求出λ的值．
（2）
与
的夹角α为钝角可得
•
＜0，且两向量
与
不共线．由此即可解出λ的取值范围．
| a |
| b |
（2）
| a |
| b |
| a |
| b |
| a |
| b |
解答：
解：（1）∵
⊥
，
=（1，-1），
=（λ，1），
∴
•
=0，即λ-1=0，解得λ=1．
（2）∵
=（1，-1），
=（λ，1），
与
的夹角α为钝角
∴
•
＜0，且两向量
与
不共线．
又
•
=λ-1，可得λ＜1．
又λ=-1时，
与
的夹角α为平角，可得λ＜1且λ≠-1．
λ的取值范围为λ＜1且λ≠-1．
| a |
| b |
| a |
| b |
∴
| a |
| b |
（2）∵
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
又
| a |
| b |
又λ=-1时，
| a |
| b |
λ的取值范围为λ＜1且λ≠-1．
点评：本题主要考查垂直的条件与夹角为钝角的条件，根据相应的基础知识将条件转化成等式或不等式是此类题的常规思路．
练习册系列答案
相关题目
在如图所示的几何体中，四边形ABCD为正方形，△ABE为直角三角形，∠BAE=90°，且AD⊥AE．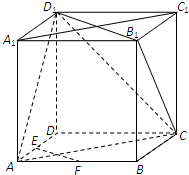
如图，在正方体ABCD-A1B1C1D1中，E、F分别为棱AD、AB的中点．