题目内容
一个袋子中有3个红球和2个黄球,5个球除颜色外完全相同,甲、乙两人先后不放回地从中各取1个球.规定:若两人取得的球的颜色相同则甲获胜,否则乙获胜.
(1)求两个人都取到黄球的概率;
(2)计算甲获胜的概率.
(1)求两个人都取到黄球的概率;
(2)计算甲获胜的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:设3个红球编号为1、2、3;两个黄球编号为4、5.求出一切可能结果的总数,
(1)求出两个人都取到黄球的取法数,代入古典概型概率计算公式,可得答案.
(2)求了两人取得的球的颜色相同的取法数,代入古典概型概率计算公式,可得答案.
(1)求出两个人都取到黄球的取法数,代入古典概型概率计算公式,可得答案.
(2)求了两人取得的球的颜色相同的取法数,代入古典概型概率计算公式,可得答案.
解答:
解:设3个红球编号为1、2、3;两个黄球编号为4、5.
则一切可能结果组成的基本事件有:
(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、
(2,4)、(2,5)、(3,4)、(3,5)、(4,5)共10个.…(2分)
(1)两个人都取得黄球的事件有(4,5)共1个.
因此两个人都取得黄球概率为P=
…((6分)
(2)两个人取得相同颜色球的事件有(1,2)、(1,3)、(2,3)、(4,5)共4个
故甲获胜的概率为P=
=
.…(9分)
则一切可能结果组成的基本事件有:
(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、
(2,4)、(2,5)、(3,4)、(3,5)、(4,5)共10个.…(2分)
(1)两个人都取得黄球的事件有(4,5)共1个.
因此两个人都取得黄球概率为P=
| 1 |
| 10 |
(2)两个人取得相同颜色球的事件有(1,2)、(1,3)、(2,3)、(4,5)共4个
故甲获胜的概率为P=
| 4 |
| 10 |
| 2 |
| 5 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
相关题目
 在如图所示的几何体中,四边形ABCD为正方形,△ABE为直角三角形,∠BAE=90°,且AD⊥AE.
在如图所示的几何体中,四边形ABCD为正方形,△ABE为直角三角形,∠BAE=90°,且AD⊥AE. 已知如图,△ABC是边长为1的正三角形,PA⊥平面ABC,且
已知如图,△ABC是边长为1的正三角形,PA⊥平面ABC,且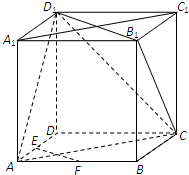 如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD、AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD、AB的中点.