题目内容
设△ABC的内角A,B,C所对的边分别为a,b,c,若c(1+cosA)=
a•sinC
(1)求角A的大小;
(2)若a=2,△ABC的面积为
,求△ABC的周长.
| 3 |
(1)求角A的大小;
(2)若a=2,△ABC的面积为
| 3 |
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(1)已知等式利用正弦定理化简,根据sinC不为0,利用两角和与差的正弦函数公式变形,求出A的度数即可;
(2)由a,以及cosA的值,利用余弦定理列出关系式得到b2+c2-bc=4,再利用三角形面积公式列出关系式,将已知面积及sinA代入求出bc=4,两式联立求出b+c的值,由a+b+c即可求出三角形ABC周长.
(2)由a,以及cosA的值,利用余弦定理列出关系式得到b2+c2-bc=4,再利用三角形面积公式列出关系式,将已知面积及sinA代入求出bc=4,两式联立求出b+c的值,由a+b+c即可求出三角形ABC周长.
解答:
解:(1)由已知及正弦定理得sinC(1+cosA)=
sinAsinC,
∵sinC≠0,∴1+cosA=
sinA,即
sinA-cosA=2(
sinA-
cosA)=2sin(A-
)=1,
∴A-
=
或A-
=
(舍去),
∴A=
;
(2)∵a=2,cosA=cos
=
,
由余弦定理得:a2=b2+c2-2bccosA,即b2+c2-bc=4,①
∵△ABC的面积为
,即
bcsinA=
bc=
,
∴bc=4,②
联立①②得:(b+c)2=4+3bc=16,
∴b+c=4,
则△ABC周长为a+b+c=2+4=6.
| 3 |
∵sinC≠0,∴1+cosA=
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴A-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴A=
| π |
| 3 |
(2)∵a=2,cosA=cos
| π |
| 3 |
| 1 |
| 2 |
由余弦定理得:a2=b2+c2-2bccosA,即b2+c2-bc=4,①
∵△ABC的面积为
| 3 |
| 1 |
| 2 |
| ||
| 4 |
| 3 |
∴bc=4,②
联立①②得:(b+c)2=4+3bc=16,
∴b+c=4,
则△ABC周长为a+b+c=2+4=6.
点评:此题考查了正弦、余弦定理,三角形面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个平面将空间分成两部分,两个平面将空间最多分成四部分,三个平面最多将空间分成八部分,…,由此猜测n(n∈N+)个平面最多将空间分成( )
| A、2n部分 | ||
| B、n2部分 | ||
| C、2n部分 | ||
D、
|
二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为( )
| A、{x|x>3或x<-2} |
| B、{x|x>2或x<-3} |
| C、{x|-2<x<3} |
| D、{x|-3<x<2} |
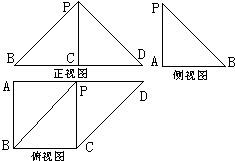 如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( )
如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( ) 选修4-1:几何证明选讲
选修4-1:几何证明选讲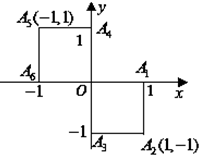 小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就去打球;若X=0就去唱歌;若X<0就去下棋.
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就去打球;若X=0就去唱歌;若X<0就去下棋.