题目内容
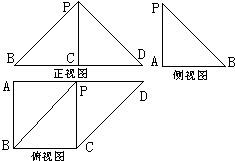 如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( )
如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由三视图知几何体为四棱锥与三棱锥的组合体,画出其直观图,判断几何体的高,计算底面面积,代入体积公式计算.
解答:
 解:由三视图知几何体为四棱锥与三棱锥的组合体,其直观图如图:
解:由三视图知几何体为四棱锥与三棱锥的组合体,其直观图如图:
根据三视图中正视图是一等腰直角三角形,且斜边BD长为2,∴棱锥的高为1,
底面直角梯形的底边长分别为1、2,高为1,∴底面面积为
×1=
,
∴几何体的体积V=
×
×1=
.
故选A.
 解:由三视图知几何体为四棱锥与三棱锥的组合体,其直观图如图:
解:由三视图知几何体为四棱锥与三棱锥的组合体,其直观图如图:根据三视图中正视图是一等腰直角三角形,且斜边BD长为2,∴棱锥的高为1,
底面直角梯形的底边长分别为1、2,高为1,∴底面面积为
| 1+2 |
| 2 |
| 3 |
| 2 |
∴几何体的体积V=
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
故选A.
点评:本题考查了由三视图求几何体的体积,解题的关键是由三视图判断几何体的形状及数据所对应的几何量.

练习册系列答案
相关题目
若16-x2≥0,则( )
| A、0≤x≤4 |
| B、-4≤x≤0 |
| C、-4≤x≤4 |
| D、x≤-4或x≥4 |
方程ax2+2x+1=0恰有一个负实根,则a的取值范围为( )
| A、a<0 | B、a≤0 |
| C、a>0 | D、a=0 |
已知f(x)是定义在R上的偶函数,且对任意x∈R,总有f(x+2)=-f(x)成立,则f(19)=( )
| A、-2 | B、-1 | C、0 | D、19 |
先后抛掷一枚质地均匀的硬币3次,有2次正面朝上的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
从某班50名学生中抽取6名学生进行视力状况的统计分析,下列说法正确的是( )
| A、50名学生是总体 |
| B、每个被调查的学生是个体 |
| C、抽取的6名学生的视力是一个样本 |
| D、抽取的6名学生的视力是样本容量 |
 设函数f(x)=|x2-4x-5|.
设函数f(x)=|x2-4x-5|.