题目内容
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为
,且各局胜负相互独立.求:
(Ⅰ)打满4局比赛还未停止的概率;
(Ⅱ)比赛停止时已打局数ξ的分布列与期望Eξ.
| 1 |
| 2 |
(Ⅰ)打满4局比赛还未停止的概率;
(Ⅱ)比赛停止时已打局数ξ的分布列与期望Eξ.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(Ⅰ)令Ak,Bk,Ck分别表示甲、乙、丙在第k局中获胜,由独立事件同时发生与互斥事件至少有一个发生的概率公式,能求出打满4局比赛还未停止的概率.
(Ⅱ)由题设知ξ的所有可能值为2,3,4,5,6,利用独立事件同时发生与互斥事件至少有一个发生的概率公式分别求出P(ξ=2),P(ξ=3),P(ξ=4),P(ξ=5),P(ξ=6),由此能求出比赛停止时已打局数ξ的分布列与期望Eξ.
(Ⅱ)由题设知ξ的所有可能值为2,3,4,5,6,利用独立事件同时发生与互斥事件至少有一个发生的概率公式分别求出P(ξ=2),P(ξ=3),P(ξ=4),P(ξ=5),P(ξ=6),由此能求出比赛停止时已打局数ξ的分布列与期望Eξ.
解答:
(本小题满分14分)
解:令Ak,Bk,Ck分别表示甲、乙、丙在第k局中获胜.
(Ⅰ)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,
打满4局比赛还未停止的概率为:
P(A1C2B3A4)+P(B1C2A3B4)=
+
=
.…(6分) (各3分)
(Ⅱ)由题设知ξ的所有可能值为2,3,4,5,6,
且P(ξ=2)=P(A1A2)+P(B1B2)=
+
=
,
P(ξ=3)=P(A1C2C3)+P(B1C2C3)=
+
=
,
P(ξ=4)=P(A1C2B3B4)+P(B1C2A3A4)=
+
=
,
P(ξ=5)=P(A1C2B3A4A5)+P(B1C2A3B4B5)=
+
=
,
P(ξ=6)=P(A1C2B3A4C5)+P(B1C2A3B4C5)=
+
=
,…(11分)
故ξ的布列为
∴Eξ=2×
+3×
+4×
+5×
+6×
=
.…(14分)
解:令Ak,Bk,Ck分别表示甲、乙、丙在第k局中获胜.
(Ⅰ)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,
打满4局比赛还未停止的概率为:
P(A1C2B3A4)+P(B1C2A3B4)=
| 1 |
| 24 |
| 1 |
| 24 |
| 1 |
| 8 |
(Ⅱ)由题设知ξ的所有可能值为2,3,4,5,6,
且P(ξ=2)=P(A1A2)+P(B1B2)=
| 1 |
| 22 |
| 1 |
| 22 |
| 1 |
| 2 |
P(ξ=3)=P(A1C2C3)+P(B1C2C3)=
| 1 |
| 23 |
| 1 |
| 23 |
| 1 |
| 4 |
P(ξ=4)=P(A1C2B3B4)+P(B1C2A3A4)=
| 1 |
| 24 |
| 1 |
| 24 |
| 1 |
| 8 |
P(ξ=5)=P(A1C2B3A4A5)+P(B1C2A3B4B5)=
| 1 |
| 25 |
| 1 |
| 25 |
| 1 |
| 16 |
P(ξ=6)=P(A1C2B3A4C5)+P(B1C2A3B4C5)=
| 1 |
| 25 |
| 1 |
| 25 |
| 1 |
| 16 |
故ξ的布列为
| ξ | 2 | 3 | 4 | 5 | 6 | ||||||||||
P |
|
|
|
|
|
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 16 |
| 47 |
| 16 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望,是中档题,解题时要合理运用独立事件同时发生与互斥事件至少有一个发生的概率公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若函数y=2x-2+3的图象恒过点P,则点P为( )
| A、(2,3) |
| B、(1,1) |
| C、(0,1) |
| D、(2,4) |
先后抛掷一枚质地均匀的硬币3次,有2次正面朝上的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
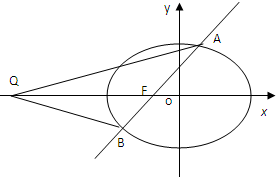 已知椭圆C:
已知椭圆C: