题目内容
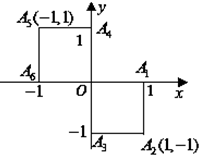 小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就去打球;若X=0就去唱歌;若X<0就去下棋.
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就去打球;若X=0就去唱歌;若X<0就去下棋.(Ⅰ)分别求小波去下棋的概率和不去唱歌的概率.
(Ⅱ)写出数量积X的所有可能取值,并求X分布列与数学期望.
考点:离散型随机变量的期望与方差,等可能事件的概率
专题:概率与统计
分析:(Ⅰ)由题设求出X的所有可能取值的种数,对取出两个向量的数量积进行计算,求出X的所有可能取值,找出X<0的次数,用古典概型的概率能求出小波去下棋的概率;再找出X=0的次数,先求出小波去唱歌的概率,由对立事件的概率求法能求出小波不去唱歌的概率.
(Ⅱ)由题设知X的所有可能取值为-2,-1,0,1,分别求出P(X=-2),P(X=-1),P(X=0),P(X=1),由此能求出X的分布列和数学期望.
(Ⅱ)由题设知X的所有可能取值为-2,-1,0,1,分别求出P(X=-2),P(X=-1),P(X=0),P(X=1),由此能求出X的分布列和数学期望.
解答:
解:(Ⅰ)由题设知X的所有可能取值,
即从
,
,
,
,
,
这六个向量中任取两个,
共有
=15种.…(1分)
如下表:
而对取出两个向量的数量积进行计算,
得到X的所有可能取值为-2,-1,0,1,…(3分)
求小波去下棋的概率,这是古典概型,
只需找出总的事件数有
种,
∵X<0就去下棋,只需在上表计算结果中,找出小于零的次数为7,…(4分)
有古典概型的概率求法知:小波去下棋的概率为P1=
,…(5分)
小波不去唱歌的概率,它的对立事件为,去唱歌,而X=0就去唱歌,
在上表中,X=0共有四次,故去唱歌的概率为P2=
,
有对立事件的概率求法知:小波不去唱歌的概率P=1-P2=1-
=
.…(6分)
(Ⅱ)由上表可知X的所有可能取值为-2,-1,0,1,
数量积为-2的只有一种,数量积为-1的有六种,数量积为0的有四种,数量积为1的有四种,
所有可能的情况共有15种.
∴P(X=-2)=
,
P(X=-1)=
=
,
P(X=0)=
,
P(X=1)=
.(每个1分) (4分)
∴X的分布列为:
(5分)
EX=-2×
+(-1)×
+0×
+1×
=-
.(6分)
即从
| OA1 |
| OA2 |
| OA3 |
| OA4 |
| OA5 |
| OA6 |
共有
| C | 2 6 |
如下表:
|
|
|
|
|
|
| ||||||||||||||||
| 1 | 0 | 0 | -1 | -1 | |||||||||||||||||
| 1 | -1 | -2 | -1 | ||||||||||||||||||
| -1 | -1 | 0 | |||||||||||||||||||
| 1 | 0 | ||||||||||||||||||||
| 1 | |||||||||||||||||||||
|
得到X的所有可能取值为-2,-1,0,1,…(3分)
求小波去下棋的概率,这是古典概型,
只需找出总的事件数有
| C | 2 6 |
∵X<0就去下棋,只需在上表计算结果中,找出小于零的次数为7,…(4分)
有古典概型的概率求法知:小波去下棋的概率为P1=
| 7 |
| 15 |
小波不去唱歌的概率,它的对立事件为,去唱歌,而X=0就去唱歌,
在上表中,X=0共有四次,故去唱歌的概率为P2=
| 4 |
| 15 |
有对立事件的概率求法知:小波不去唱歌的概率P=1-P2=1-
| 4 |
| 15 |
| 11 |
| 15 |
(Ⅱ)由上表可知X的所有可能取值为-2,-1,0,1,
数量积为-2的只有一种,数量积为-1的有六种,数量积为0的有四种,数量积为1的有四种,
所有可能的情况共有15种.
∴P(X=-2)=
| 1 |
| 15 |
P(X=-1)=
| 6 |
| 15 |
| 2 |
| 5 |
P(X=0)=
| 4 |
| 15 |
P(X=1)=
| 4 |
| 15 |
∴X的分布列为:
| X | -2 | -1 | 0 | 1 | ||||||||
| P |
|
|
|
|
EX=-2×
| 1 |
| 15 |
| 2 |
| 5 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
| 15 |
点评:本题考查离散型随机变量的分布列和数学期望的求法,是历年高考的必考题型之一,解题时要注意排列组合知识的合理运用,是中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
方程ax2+2x+1=0恰有一个负实根,则a的取值范围为( )
| A、a<0 | B、a≤0 |
| C、a>0 | D、a=0 |
已知等差数列的前n项和为18,若S3=1,an+an-1+an-2=3,则n的值为( )
| A、9 | B、21 | C、27 | D、36 |
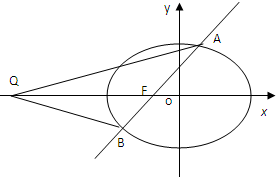 已知椭圆C:
已知椭圆C: