题目内容
已知角α的顶点在原点,始边与x轴的非负半轴重合,终边经过点P(-3,
).
(Ⅰ)求
的值:
(Ⅱ)求tan2α的值.
| 3 |
(Ⅰ)求
tan(-α)+sin(
| ||
| cos(π-α)sin(-π-α) |
(Ⅱ)求tan2α的值.
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(Ⅰ)由α的终点经过P点,根据P坐标,利用任意角的三角函数定义求出sinα,cosα,tanα的值,原式利用诱导公式化简,变形后将各自的值代入计算即可求出值;
(Ⅱ)原式利用二倍角的正切函数公式化简,将tanα的值代入计算即可求出值.
(Ⅱ)原式利用二倍角的正切函数公式化简,将tanα的值代入计算即可求出值.
解答:
解:(Ⅰ)∵角α的终边经过P(-3,
),
∴sinα=
=
,cosα=-
=-
,tanα=-
,
则原式=
=
-
=
-2=-
;
(Ⅱ)∵tanα=-
,
∴tan2α=
=
=-
.
| 3 |
∴sinα=
| ||||
|
| 1 |
| 2 |
| 3 | ||
2
|
| ||
| 2 |
| ||
| 3 |
则原式=
| -tanα+cosα |
| -cosαsinα |
| 1 |
| cos2α |
| 1 |
| sinα |
| 4 |
| 3 |
| 2 |
| 3 |
(Ⅱ)∵tanα=-
| ||
| 3 |
∴tan2α=
| 2tanα |
| 1-tan2α |
2×(-
| ||||
1-(-
|
| 3 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
不等式2x2+mx+n>0的解集是{x|x>3或x<-2},则二次函数y=2x2+mx+n的表达式是( )
| A、y=2x2+2x+12 |
| B、y=2x2-2x+12 |
| C、y=2x2+2x-12 |
| D、y=2x2-2x-12 |
已知f(x)是定义在R上的偶函数,且对任意x∈R,总有f(x+2)=-f(x)成立,则f(19)=( )
| A、-2 | B、-1 | C、0 | D、19 |
从某班50名学生中抽取6名学生进行视力状况的统计分析,下列说法正确的是( )
| A、50名学生是总体 |
| B、每个被调查的学生是个体 |
| C、抽取的6名学生的视力是一个样本 |
| D、抽取的6名学生的视力是样本容量 |
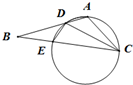 选修4-1:几何证明选讲
选修4-1:几何证明选讲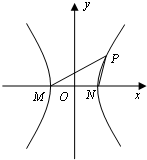 已知双曲线x2-y2=2013的左、右顶点分别为M、N,点P是双曲线上异于M、N的任意一点.
已知双曲线x2-y2=2013的左、右顶点分别为M、N,点P是双曲线上异于M、N的任意一点.