题目内容
二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为( )
| A、{x|x>3或x<-2} |
| B、{x|x>2或x<-3} |
| C、{x|-2<x<3} |
| D、{x|-3<x<2} |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:由于二次方程ax2+bx+c=0的两根为-2,3,可得
化为
.由于a<0,因此ax2+bx+c>0可化为x2+
x+
<0,即x2-x-6<0.解出即可.
|
|
| b |
| a |
| c |
| a |
解答:
解:∵二次方程ax2+bx+c=0的两根为-2,3,
∴
化为
∵a<0,∴ax2+bx+c>0可化为x2+
x+
<0,
即x2-x-6<0.
解得-2<x<3.
∴ax2+bx+c>0的解集为{x|-2<x<3}.
故选:C.
∴
|
化为
|
∵a<0,∴ax2+bx+c>0可化为x2+
| b |
| a |
| c |
| a |
即x2-x-6<0.
解得-2<x<3.
∴ax2+bx+c>0的解集为{x|-2<x<3}.
故选:C.
点评:本题考查了一元二次方程的根与系数的关系、一元二次不等式的解法,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
方程ax2+2x+1=0恰有一个负实根,则a的取值范围为( )
| A、a<0 | B、a≤0 |
| C、a>0 | D、a=0 |
先后抛掷一枚质地均匀的硬币3次,有2次正面朝上的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
从某班50名学生中抽取6名学生进行视力状况的统计分析,下列说法正确的是( )
| A、50名学生是总体 |
| B、每个被调查的学生是个体 |
| C、抽取的6名学生的视力是一个样本 |
| D、抽取的6名学生的视力是样本容量 |
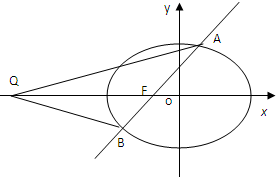 已知椭圆C:
已知椭圆C: